1552. Magnetic Force Between Two Balls

Posted on Edited on In

1552. Magnetic Force Between Two Balls

Description

In the universe Earth C-137, Rick discovered a special form of magnetic force between two balls if they are put in his new invented basket. Rick has n empty baskets, the i^th basket is at position[i], Morty has m balls and needs to distribute the balls into the baskets such that the minimum magnetic force between any two balls is maximum .

Rick stated that magnetic force between two different balls at positions x and y is |x - y|.

Given the integer array position and the integer m. Return the required force.

Example 1:

1
2
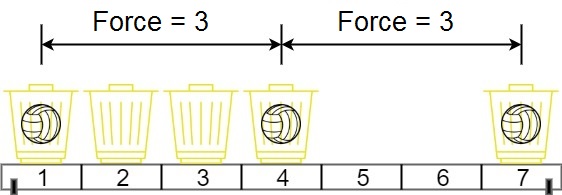
3
Input: position = [1,2,3,4,7], m = 3
Output: 3
Explanation: Distributing the 3 balls into baskets 1, 4 and 7 will make the magnetic force between ball pairs [3, 3, 6]. The minimum magnetic force is 3. We cannot achieve a larger minimum magnetic force than 3.

Example 2:

1
2
3
Input: position = [5,4,3,2,1,1000000000], m = 2
Output: 999999999
Explanation: We can use baskets 1 and 1000000000.

Constraints:

  • n == position.length
  • 2 <= n <= 10^5
  • 1 <= position[i] <= 10^9
  • All integers in position are distinct .
  • 2 <= m <= position.length

Hints/Notes

Solution

Language: C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    int maxDistance(vector<int>& position, int m) {
        ranges::sort(position);
        int n = position.size();
        int low = 0, high = ceil(position[n - 1] / (m - 1.0)) + 1;
        while (low + 1 < high) {
            int mid = (low + high) / 2;
            if (check(mid, position, m)) {
                low = mid;
            } else {
                high = mid;
            }
        }
        return low;
    }

    bool check(int interval, vector<int>& position, int m) {
        int placed = 1, prev = position[0];
        for (int i = 1; i < position.size(); i++) {
            if (position[i] >= prev + interval) {
                placed++;
                prev = position[i];
            }
            if (placed >= m) {
                return true;
            }
        }
        return false;
    }
};