935. Knight Dialer

Posted on Edited on In

935. Knight Dialer

Description

The chess knight has a unique movement ,it may move two squares vertically and one square horizontally, or two squares horizontally and one square vertically (with both forming the shape of an L ). The possible movements of chess knight are shown in this diagram:

A chess knight can move as indicated in the chess diagram below: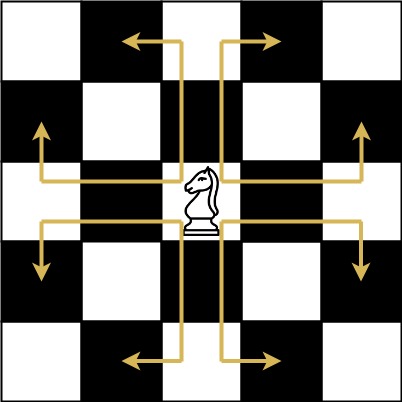

We have a chess knight and a phone pad as shown below, the knight can only stand on a numeric cell (i.e. blue cell).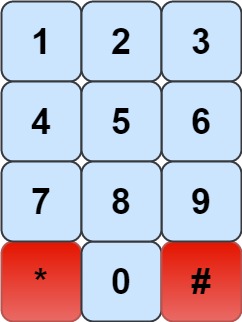

Given an integer n, return how many distinct phone numbers of length n we can dial.

You are allowed to place the knight on any numeric cell initially and then you should perform n - 1 jumps to dial a number of length n. All jumps should be valid knight jumps.

As the answer may be very large, return the answer modulo 10^9 + 7.

Example 1:

1
2
3
Input: n = 1
Output: 10
Explanation: We need to dial a number of length 1, so placing the knight over any numeric cell of the 10 cells is sufficient.

Example 2:

1
2
3
Input: n = 2
Output: 20
Explanation: All the valid number we can dial are [04, 06, 16, 18, 27, 29, 34, 38, 40, 43, 49, 60, 61, 67, 72, 76, 81, 83, 92, 94]

Example 3:

1
2
3
Input: n = 3131
Output: 136006598
Explanation: Please take care of the mod.

Constraints:

  • 1 <= n <= 5000

Hints/Notes

Solution

Language: C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
class Solution {
public:
    // for each number, the number of following choices:
    // 0 ~ 3: 2
    // 4, 6: 3
    // 7 ~ 9: 2
    // it's like matrix calculation
    const int MOD = 1e9 + 7;
    long matrix[10][10] = {
    //   0, 1, 2, 3, 4, 5, 6, 7, 8, 9
        {0, 0, 0, 0, 1, 0, 1, 0, 0, 0}, // 0
        {0, 0, 0, 0, 0, 0, 1, 0, 1, 0}, // 1
        {0, 0, 0, 0, 0, 0, 0, 1, 0, 1}, // 2
        {0, 0, 0, 0, 1, 0, 0, 0, 1, 0}, // 3
        {1, 0, 0, 1, 0, 0, 0, 0, 0, 1}, // 4
        {0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, // 5
        {1, 1, 0, 0, 0, 0, 0, 1, 0, 0}, // 6
        {0, 0, 1, 0, 0, 0, 1, 0, 0, 0}, // 7
        {0, 1, 0, 1, 0, 0, 0, 0, 0, 0}, // 8
        {0, 0, 1, 0, 1, 0, 0, 0, 0, 0}, // 9
    };

    int knightDialer(int n) {
        long pow[10][10], res[10][10]{};
        memcpy(pow, matrix, sizeof(matrix));
        for (int i = 0; i < 10; i++) {
            res[i][i] = 1;
        }
        n -= 1;
        while (n > 0) {
            if (n % 2) {
                mul(pow, res);
            }
            mul(pow, pow);
            n /= 2;
        }
        int ans = 0;
        for (int i = 0; i < 10; i++) {
            for (int j = 0; j < 10; j++) {
                ans = (ans + res[i][j]) % MOD;
            }
        }
        return ans;
    }

    void mul(long pow[10][10], long res[10][10]) {
        long new_res[10][10]{};
        for (int i = 0; i < 10; i++) {
            for (int j = 0; j < 10; j++) {
                for (int k = 0; k < 10; k++) {
                    new_res[i][j] = (new_res[i][j] + pow[i][k] * res[k][j]) % MOD;
                }
            }
        }
        memcpy(res, new_res, sizeof(new_res));
    }
};