1522. Diameter of N-Ary Tree

Posted on Edited on In

1522. Diameter of N-Ary Tree

Description

Given a root of an N-ary tree, you need to compute the length of the diameter of the tree.

The diameter of an N-ary tree is the length of the longest path between any two nodes in the tree. This path may or may not pass through the root.

(Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value.)

Example 1:

1
2
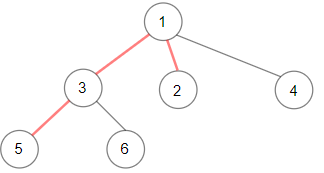
3
Input: root = [1,null,3,2,4,null,5,6]
Output: 3
Explanation: Diameter is shown in red color.

Example 2:

1
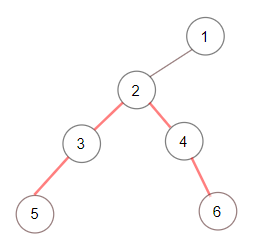
2
Input: root = [1,null,2,null,3,4,null,5,null,6]
Output: 4

Example 3:

1
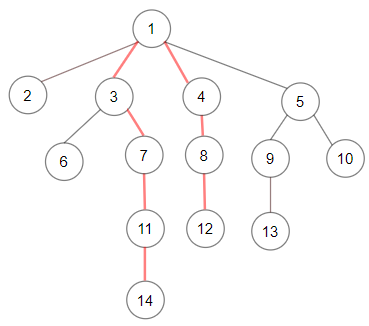
2
Input: root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
Output: 7

Constraints:

  • The depth of the n-ary tree is less than or equal to 1000.
  • The total number of nodes is between [1, 10^4].

Hints/Notes

Solution

Language: C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val) {
        val = _val;
    }

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
public:
    int res = 0;

    int diameter(Node* root) {
        dfs(root);
        return res;
    }

    int dfs(Node* root) {
        if (!root) {
            return 0;
        }
        int mx1 = 0, mx2 = 0;
        for (auto& node : root->children) {
            int cur = dfs(node);
            if (cur >= mx1) {
                mx2 = mx1;
                mx1 = cur;
            } else if (cur > mx2) {
                mx2 = cur;
            }
        }
        res = max(res, mx1 + mx2);
        return mx1 + 1;
    }
};