1102. Path With Maximum Minimum Value

Posted on Edited on In

1102. Path With Maximum Minimum Value

Description

Given an m x n integer matrix grid, return the maximum score of a path starting at (0, 0) and ending at (m - 1, n - 1) moving in the 4 cardinal directions.

The score of a path is the minimum value in that path.

  • For example, the score of the path 8 → 4 → 5 → 9 is 4.

Example 1:

1
2
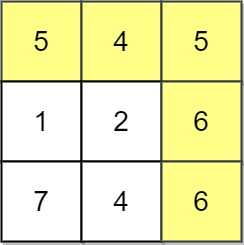
3
Input: grid = [[5,4,5],[1,2,6],[7,4,6]]
Output: 4
Explanation: The path with the maximum score is highlighted in yellow.

Example 2:

1
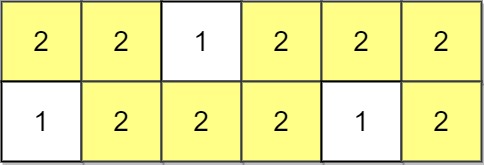
2
Input: grid = [[2,2,1,2,2,2],[1,2,2,2,1,2]]
Output: 2

Example 3:

1
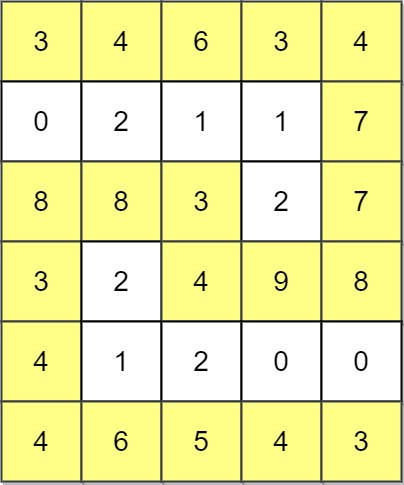
2
Input: grid = [[3,4,6,3,4],[0,2,1,1,7],[8,8,3,2,7],[3,2,4,9,8],[4,1,2,0,0],[4,6,5,4,3]]
Output: 3

Constraints:

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 100
  • 0 <= grid[i][j] <= 10^9

Hints/Notes

Solution

Language: C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    static constexpr int DIRs[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};

    int maximumMinimumPath(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        priority_queue<vector<int>, vector<vector<int>>, less<vector<int>>> pq;
        int res = INT_MAX;
        pq.push({grid[0][0], 0, 0});
        grid[0][0] = -1;
        while (!pq.empty()) {
            auto tri = pq.top();
            pq.pop();
            int val = tri[0], x = tri[1], y = tri[2];
            res = min(res, val);
            if (x == m - 1 && y == n - 1) {
                return res;
            }
            for (int k = 0; k < 4; k++) {
                int dx = x + DIRs[k][0], dy = y + DIRs[k][1];
                if (dx >= 0 && dx < m && dy >= 0 && dy < n && grid[dx][dy] >= 0) {
                    pq.push({grid[dx][dy], dx, dy});
                    grid[dx][dy] = -1;
                }
            }
        }
        return -1;
    }
};