2673. Make Costs of Paths Equal in a Binary Tree

Posted on Edited on In

2673. Make Costs of Paths Equal in a Binary Tree

Description

You are given an integer n representing the number of nodes in a perfect binary tree consisting of nodes numbered from 1 to n. The root of the tree is node 1 and each node i in the tree has two children where the left child is the node 2 * i and the right child is 2 * i + 1.

Each node in the tree also has a cost represented by a given 0-indexed integer array cost of size n where cost[i] is the cost of node i + 1. You are allowed to increment the cost of any node by 1 any number of times.

Return the minimum number of increments you need to make the cost of paths from the root to each leaf node equal.

Note :

  • A perfect binary tree is a tree where each node, except the leaf nodes, has exactly 2 children.
  • The cost of a path is the sum of costs of nodes in the path.

Example 1:

1
2
3
4
5
6
7
8
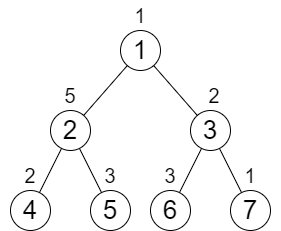
9
Input: n = 7, cost = [1,5,2,2,3,3,1]
Output: 6
Explanation: We can do the following increments:
- Increase the cost of node 4 one time.
- Increase the cost of node 3 three times.
- Increase the cost of node 7 two times.
Each path from the root to a leaf will have a total cost of 9.
The total increments we did is 1 + 3 + 2 = 6.
It can be shown that this is the minimum answer we can achieve.

Example 2:

1
2
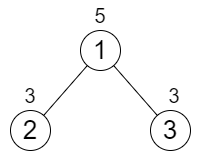
3
Input: n = 3, cost = [5,3,3]
Output: 0
Explanation: The two paths already have equal total costs, so no increments are needed.

Constraints:

  • 3 <= n <= 10^5
  • n + 1 is a power of 2
  • cost.length == n
  • 1 <= cost[i] <= 10^4

Hints/Notes

Solution

Language: C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int res = 0;
    vector<int> paths;

    int minIncrements(int n, vector<int>& cost) {
        helper(1, cost);
        return res;
    }

    int helper(int index, vector<int>& cost) {
        if (index * 2 > cost.size()) {
            return cost[index - 1];
        }
        int left = helper(index * 2, cost);
        int right = helper(index * 2 + 1, cost);
        if (left != right) {
            res += abs(left - right);
        }
        return max(left, right) + cost[index - 1];
    }
};