296. Best Meeting Point

Posted on Edited on In

296. Best Meeting Point

Description

Given an m x n binary grid grid where each 1 marks the home of one friend, return the minimal total travel distance .

The total travel distance is the sum of the distances between the houses of the friends and the meeting point.

The distance is calculated using Manhattan Distance, where distance(p1, p2) = |p2.x - p1.x| + |p2.y - p1.y|.

Example 1:

1
2
3
4
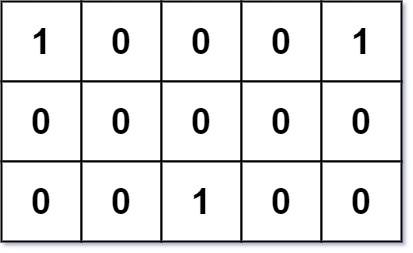
5
Input: grid = [[1,0,0,0,1],[0,0,0,0,0],[0,0,1,0,0]]
Output: 6
Explanation: Given three friends living at (0,0), (0,4), and (2,2).
The point (0,2) is an ideal meeting point, as the total travel distance of 2 + 2 + 2 = 6 is minimal.
So return 6.

Example 2:

1
2
Input: grid = [[1,1]]
Output: 1

Constraints:

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 200
  • grid[i][j] is either 0 or 1.
  • There will be at least two friends in the grid.

Hints/Notes

Solution

Language: C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    int minTotalDistance(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        vector<int> rows, cols;
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j]) {
                    rows.push_back(i);
                    cols.push_back(j);
                }
            }
        }
        int mid = rows.size() / 2, res = 0;
        ranges::sort(cols);
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j]) {
                    res += abs(i - rows[mid]) + abs(j - cols[mid]);
                }
            }
        }
        return res;
    }
};