272. Closest Binary Search Tree Value II

Posted on Edited on In

272. Closest Binary Search Tree Value II

Description

Given the root of a binary search tree, a target value, and an integer k, return the k values in the BST that are closest to the target. You may return the answer in any order .

You are guaranteed to have only one unique set of k values in the BST that are closest to the target.

Example 1:

1
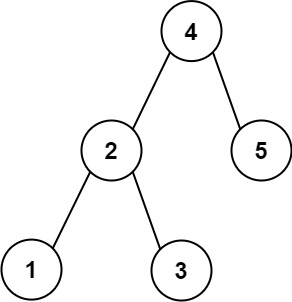
2
Input: root = [4,2,5,1,3], target = 3.714286, k = 2
Output: [4,3]

Example 2:

1
2
Input: root = [1], target = 0.000000, k = 1
Output: [1]

Constraints:

  • The number of nodes in the tree is n.
  • 1 <= k <= n <= 10^4.
  • 0 <= Node.val <= 10^9
  • -10^9 <= target <= 10^9

Follow up: Assume that the BST is balanced. Could you solve it in less than O(n) runtime (where n = total nodes)?

Hints/Notes

Solution

Language: C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> inorder;

    vector<int> closestKValues(TreeNode* root, double target, int k) {
        dfs(root);
        int size = inorder.size();
        int closestIdx = 0;
        for (int i = 1; i < size; i++) {
            if (abs(inorder[i] - target) < abs(inorder[closestIdx] - target)) {
                closestIdx = i;
            }
        }
        vector<int> res;
        int left = closestIdx, right = closestIdx + 1;
        // we are looking at (left, right)
        while (right - left - 1 < k) {
            if (left < 0) {
                res.push_back(inorder[right++]);
            } else if (right == size) {
                res.push_back(inorder[left--]);
            } else {
                if (abs(inorder[left] - target) <= abs(inorder[right] - target)) {
                    res.push_back(inorder[left--]);
                } else {
                    res.push_back(inorder[right++]);
                }
            }
        }
        return res;
    }

    void dfs(TreeNode* root) {
        if (!root) {
            return;
        }
        dfs(root->left);
        inorder.push_back(root->val);
        dfs(root->right);
    }
};