3439. Reschedule Meetings for Maximum Free Time I

Posted on Edited on In

3439. Reschedule Meetings for Maximum Free Time I

Description

You are given an integer eventTime denoting the duration of an event, where the event occurs from time t = 0 to time t = eventTime.

You are also given two integer arrays startTime and endTime, each of length n. These represent the start and end time of n non-overlapping meetings, where the i^th meeting occurs during the time [startTime[i], endTime[i]].

You can reschedule at most k meetings by moving their start time while maintaining the same duration , to maximize the longest continuous period of free time during the event.

The relative order of all the meetings should stay the same and they should remain non-overlapping.

Return the maximum amount of free time possible after rearranging the meetings.

Note that the meetings can not be rescheduled to a time outside the event.

Example 1:

1
2
3
Input: eventTime = 5, k = 1, startTime = [1,3], endTime = [2,5]

Output: 2

Explanation:

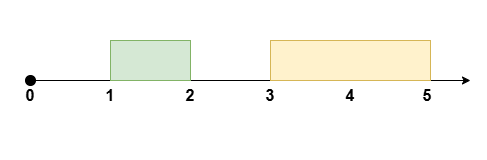
Reschedule the meeting at [1, 2] to [2, 3], leaving no meetings during the time [0, 2].

Example 2:

1
2
3
Input: eventTime = 10, k = 1, startTime = [0,2,9], endTime = [1,4,10]

Output: 6

Explanation:

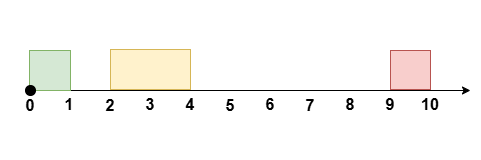
Reschedule the meeting at [2, 4] to [1, 3], leaving no meetings during the time [3, 9].

Example 3:

1
2
3
Input: eventTime = 5, k = 2, startTime = [0,1,2,3,4], endTime = [1,2,3,4,5]

Output: 0

Explanation:

There is no time during the event not occupied by meetings.

Constraints:

  • 1 <= eventTime <= 10^9
  • n == startTime.length == endTime.length
  • 2 <= n <= 10^5
  • 1 <= k <= n
  • 0 <= startTime[i] < endTime[i] <= eventTime
  • endTime[i] <= startTime[i + 1] where i lies in the range [0, n - 2].

Hints/Notes

Solution

Language: C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int maxFreeTime(int eventTime, int k, vector<int>& startTime, vector<int>& endTime) {
        vector<int> intervals;
        int n = startTime.size();
        intervals.push_back(startTime[0]);
        for (int i = 0; i < n - 1; i++) {
            intervals.push_back(startTime[i + 1] - endTime[i]);
        }
        intervals.push_back(eventTime - endTime[n - 1]);
        int res = 0, cur = 0;
        for (int i = 0; i < intervals.size(); i++) {
            cur += intervals[i];
            if (i >= k) {
                res = max(res, cur);
                cur -= intervals[i - k];
            }
        }
        return res;
    }
};