545. Boundary of Binary Tree

Posted on Edited on In

545. Boundary of Binary Tree

Description

The boundary of a binary tree is the concatenation of the root , the left boundary , the leaves ordered from left-to-right, and the reverse order of the right boundary .

The left boundary is the set of nodes defined by the following:

  • The root node’s left child is in the left boundary. If the root does not have a left child, then the left boundary is empty .
  • If a node in the left boundary and has a left child, then the left child is in the left boundary.
  • If a node is in the left boundary, has no left child, but has a right child, then the right child is in the left boundary.
  • The leftmost leaf is not in the left boundary.

The right boundary is similar to the left boundary , except it is the right side of the root’s right subtree. Again, the leaf is not part of the right boundary , and the right boundary is empty if the root does not have a right child.

The leaves are nodes that do not have any children. For this problem, the root is not a leaf.

Given the root of a binary tree, return the values of its boundary .

Example 1:

1
2
3
4
5
6
7
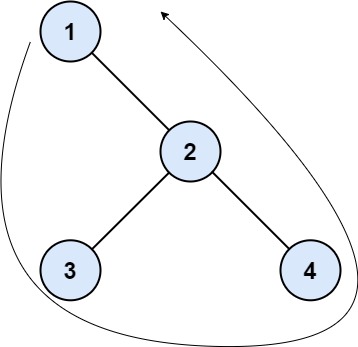
8
Input: root = [1,null,2,3,4]
Output: [1,3,4,2]
<b>Explanation:</b>
- The left boundary is empty because the root does not have a left child.
- The right boundary follows the path starting from the root's right child 2 -> 4.
  4 is a leaf, so the right boundary is [2].
- The leaves from left to right are [3,4].
Concatenating everything results in [1] + [] + [3,4] + [2] = [1,3,4,2].

Example 2:

1
2
3
4
5
6
7
8
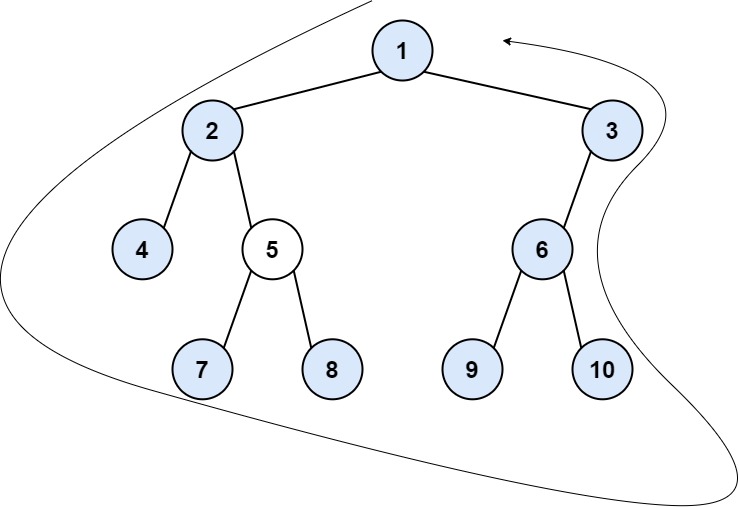
9
Input: root = [1,2,3,4,5,6,null,null,null,7,8,9,10]
Output: [1,2,4,7,8,9,10,6,3]
<b>Explanation:</b>
- The left boundary follows the path starting from the root's left child 2 -> 4.
  4 is a leaf, so the left boundary is [2].
- The right boundary follows the path starting from the root's right child 3 -> 6 -> 10.
  10 is a leaf, so the right boundary is [3,6], and in reverse order is [6,3].
- The leaves from left to right are [4,7,8,9,10].
Concatenating everything results in [1] + [2] + [4,7,8,9,10] + [6,3] = [1,2,4,7,8,9,10,6,3].

Constraints:

  • The number of nodes in the tree is in the range [1, 10^4].
  • -1000 <= Node.val <= 1000

Hints/Notes

Solution

Language: C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> boundaryOfBinaryTree(TreeNode* root) {
        vector<int> res;
        if (!root) {
            return res;
        }
        res.push_back(root->val);
        // handle the left boundary
        TreeNode* cur = root->left;
        while (cur && (cur->left || cur->right)) {
            res.push_back(cur->val);
            cur = cur->left ? cur->left : cur->right;
        }
        // handle the leaves
        stack<TreeNode*> stk;
        stk.push(root->right);
        stk.push(root->left);
        while (!stk.empty()) {
            TreeNode* cur = stk.top();
            stk.pop();
            if (!cur) {
                continue;
            }
            if (!cur->left && !cur->right) {
                res.push_back(cur->val);
            } else {
                if (cur->right) stk.push(cur->right);
                if (cur->left) stk.push(cur->left);
            }
        }
        // handle the right boundary
        cur = root->right;
        while (cur && (cur->left || cur->right)) {
            stk.push(cur);
            cur = cur->right ? cur->right : cur->left;
        }
        while (!stk.empty()) {
            res.push_back(stk.top()->val);
            stk.pop();
        }
        return res;
    }
};