490. The Maze

Posted on Edited on In

490. The Maze

Description

There is a ball in a maze with empty spaces (represented as 0) and walls (represented as 1). The ball can go through the empty spaces by rolling up, down, left or right , but it won’t stop rolling until hitting a wall. When the ball stops, it could choose the next direction.

Given the m x n maze, the ball’s start position and the destination, where start = [startrow, startcol] and destination = [destinationrow, destinationcol], return true if the ball can stop at the destination, otherwise return false.

You may assume that the borders of the maze are all walls (see examples).

Example 1:

1
2
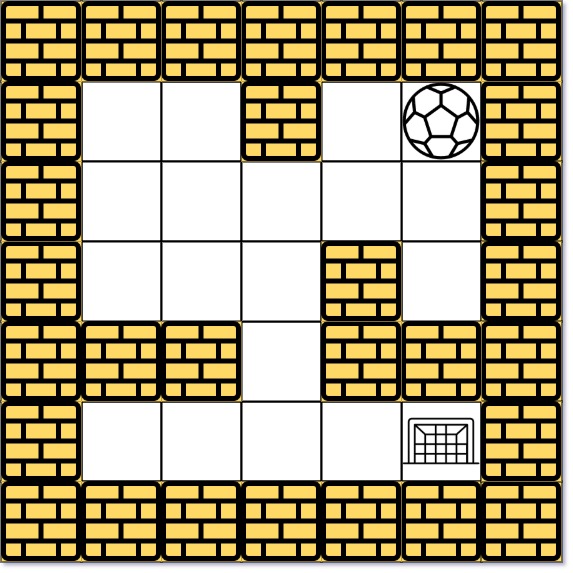
3
Input: maze = [[0,0,1,0,0],[0,0,0,0,0],[0,0,0,1,0],[1,1,0,1,1],[0,0,0,0,0]], start = [0,4], destination = [4,4]
Output: true
Explanation: One possible way is : left -> down -> left -> down -> right -> down -> right.

Example 2:

1
2
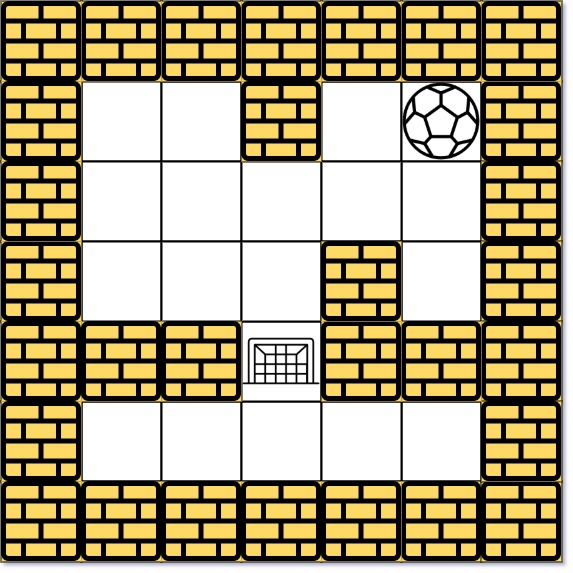
3
Input: maze = [[0,0,1,0,0],[0,0,0,0,0],[0,0,0,1,0],[1,1,0,1,1],[0,0,0,0,0]], start = [0,4], destination = [3,2]
Output: false
Explanation: There is no way for the ball to stop at the destination. Notice that you can pass through the destination but you cannot stop there.

Example 3:

1
2
Input: maze = [[0,0,0,0,0],[1,1,0,0,1],[0,0,0,0,0],[0,1,0,0,1],[0,1,0,0,0]], start = [4,3], destination = [0,1]
Output: false

Constraints:

  • m == maze.length
  • n == maze[i].length
  • 1 <= m, n <= 100
  • maze[i][j] is 0 or 1.
  • start.length == 2
  • destination.length == 2
  • 0 <= startrow, destinationrow < m
  • 0 <= startcol, destinationcol < n
  • Both the ball and the destination exist in an empty space, and they will not be in the same position initially.
  • The maze contains at least 2 empty spaces .

Hints/Notes

Solution

Language: C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    static constexpr int DIRs[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};

    bool hasPath(vector<vector<int>>& maze, vector<int>& start, vector<int>& destination) {
        int m = maze.size(), n = maze[0].size();
        if (start == destination) {
            return true;
        }
        queue<pair<int, int>> q;
        q.emplace(start[0], start[1]);
        maze[start[0]][start[1]] = -1;
        while (!q.empty()) {
            auto [x, y] = q.front();
            q.pop();
            for (int j = 0; j < 4; j++) {
                int dx = x, dy = y;
                while (dx >= 0 && dx < m && dy >= 0 && dy < n && maze[dx][dy] != 1) {
                    dx += DIRs[j][0];
                    dy += DIRs[j][1];
                }
                dx -= DIRs[j][0]; dy -= DIRs[j][1];
                if (dx == destination[0] && dy == destination[1]) {
                    return true;
                }
                if (maze[dx][dy] == 0) {
                    maze[dx][dy] = -1;
                    q.emplace(dx, dy);
                }
            }
        }
        return false;
    }
};