2271. Maximum White Tiles Covered by a Carpet

Posted on Edited on In

2271. Maximum White Tiles Covered by a Carpet

Description

You are given a 2D integer array tiles where tiles[i] = [li, ri] represents that every tile j in the range li <= j <= ri is colored white.

You are also given an integer carpetLen, the length of a single carpet that can be placed anywhere .

Return the maximum number of white tiles that can be covered by the carpet.

Example 1:

1
2
3
4
5
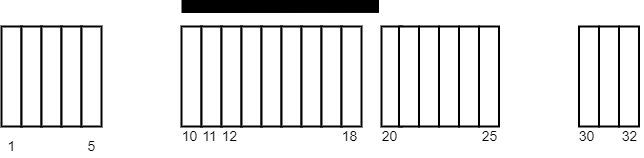
6
Input: tiles = [[1,5],[10,11],[12,18],[20,25],[30,32]], carpetLen = 10
Output: 9
Explanation: Place the carpet starting on tile 10.
It covers 9 white tiles, so we return 9.
Note that there may be other places where the carpet covers 9 white tiles.
It can be shown that the carpet cannot cover more than 9 white tiles.

Example 2:

1
2
3
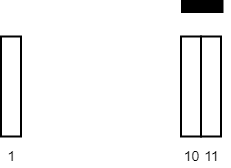
4
Input: tiles = [[10,11],[1,1]], carpetLen = 2
Output: 2
Explanation: Place the carpet starting on tile 10.
It covers 2 white tiles, so we return 2.

Constraints:

  • 1 <= tiles.length <= 5 * 10^4
  • tiles[i].length == 2s
  • 1 <= li <= ri <= 10^9
  • 1 <= carpetLen <= 10^9
  • The tiles are non-overlapping .

Hints/Notes

Solution

Language: C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    int maximumWhiteTiles(vector<vector<int>>& tiles, int carpetLen) {
        ranges::sort(tiles);
        int left = 0, cur = 0, n = tiles.size(), res = 0;
        for (int i = 0; i < n; i++) {
            int right = tiles[i][1] + 1;
            cur += tiles[i][1] - tiles[i][0] + 1;
            // at this step, we moved tiles out of the carpet, whose
            // right side is less than (right - carpetLen)
            while (tiles[left][1] < right - carpetLen) {
                cur -= tiles[left][1] - tiles[left][0] + 1;
                left++;
            }
            // now it's possible that the left is out of the carpet
            if (tiles[left][0] < right - carpetLen) {
                res = max(res, cur - (right - carpetLen - tiles[left][0]));
            } else {
                res = max(res, cur);
            }
        }
        return res;
    }
};