3378. Count Connected Components in LCM Graph

Posted on Edited on In

3378. Count Connected Components in LCM Graph

Description

You are given an array of integers nums of size n and a positive integer threshold.

There is a graph consisting of n nodes with thei^thnode having a value of nums[i]. Two nodes i and j in the graph are connected via an undirected edge if lcm(nums[i], nums[j]) <= threshold.

Return the number of connected components in this graph.

A connected component is a subgraph of a graph in which there exists a path between any two vertices, and no vertex of the subgraph shares an edge with a vertex outside of the subgraph.

The term lcm(a, b) denotes the least common multiple of a and b.

Example 1:

1
2
3
Input: nums = [2,4,8,3,9], threshold = 5

Output: 4

Explanation:

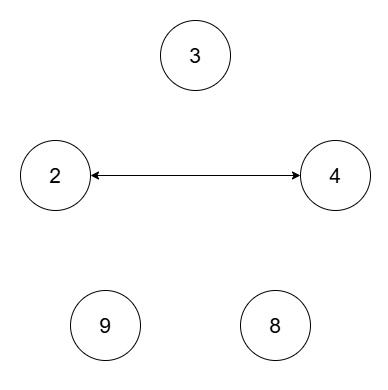
The four connected components are (2, 4), (3), (8), (9).

Example 2:

1
2
3
Input: nums = [2,4,8,3,9,12], threshold = 10

Output: 2

Explanation:

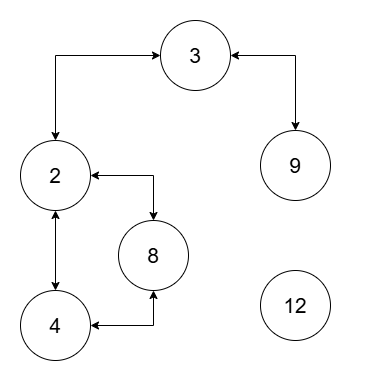
The two connected components are (2, 3, 4, 8, 9), and (12).

Constraints:

  • 1 <= nums.length <= 10^5
  • 1 <= nums[i] <= 10^9
  • All elements of nums are unique.
  • 1 <= threshold <= 2 * 10^5

Hints/Notes

Solution

Language: C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution {
public:
    vector<int> parent;

    int countComponents(vector<int>& nums, int threshold) {
        int n = nums.size();
        parent.resize(n);
        iota(parent.begin(), parent.end(), 0);
        unordered_map<int, int> m;
        for (int i = 0; i < n; i++) {
            m[nums[i]] = i;
        }
        for (int g = 1; g <= threshold; g++) {
            int min_x = -1;
            for (int i = g; i <= threshold; i += g) {
                if (m.contains(i)) {
                    min_x = i;
                    break;
                }
            }
            if (min_x == -1) {
                continue;
            }
            int fx = findRoot(m[min_x]);
            for (long long y = min_x + g; y * min_x <= (long long) g * threshold; y += g) {
                if (m.contains(y)) {
                    int fy = findRoot(m[y]);
                    if (fx != fy) {
                        parent[fy] = fx;
                        n--;
                    }
                }
            }
        }
        return n;
    }

    int findRoot(int root) {
        if (parent[root] != root) {
            parent[root] = findRoot(parent[root]);
        }
        return parent[root];
    }
};