3331. Find Subtree Sizes After Changes

Posted on Edited on In

3331. Find Subtree Sizes After Changes

Description

You are given a tree rooted at node 0 that consists of n nodes numbered from 0 to n - 1. The tree is represented by an array parent of size n, where parent[i] is the parent of node i. Since node 0 is the root, parent[0] == -1.

You are also given a string s of length n, where s[i] is the character assigned to node i.

We make the following changes on the tree one time simultaneously for all nodes x from 1 to n - 1:

  • Find the closest node y to node x such that y is an ancestor of x, and s[x] == s[y].
  • If node y does not exist, do nothing.
  • Otherwise, remove the edge between x and its current parent and make node y the new parent of x by adding an edge between them.

Return an array answer of size n where answer[i] is the size of the subtree rooted at node i in the final tree.

Example 1:

1
2
3
Input: parent = [-1,0,0,1,1,1], s = "abaabc"

Output: [6,3,1,1,1,1]

Explanation:

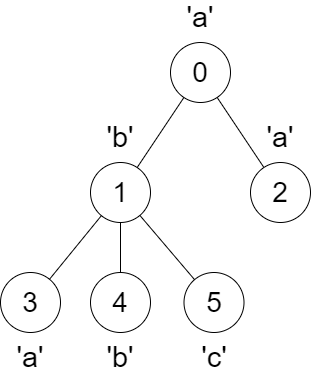
The parent of node 3 will change from node 1 to node 0.

Example 2:

1
2
3
Input: parent = [-1,0,4,0,1], s = "abbba"

Output: [5,2,1,1,1]

Explanation:

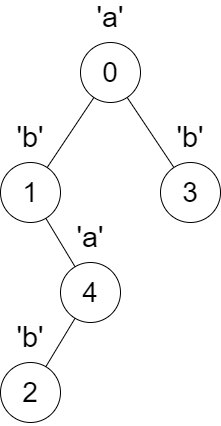
The following changes will happen at the same time:

  • The parent of node 4 will change from node 1 to node 0.
  • The parent of node 2 will change from node 4 to node 1.

Constraints:

  • n == parent.length == s.length
  • 1 <= n <= 10^5
  • 0 <= parent[i] <= n - 1 for all i >= 1.
  • parent[0] == -1
  • parent represents a valid tree.
  • s consists only of lowercase English letters.

Hints/Notes

Solution

Language: C++

One DFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    vector<unordered_set<int>> tree;
    array<int, 26> m;
    vector<int> res;

    vector<int> findSubtreeSizes(vector<int>& parent, string s) {
        int n = s.size();
        fill(m.begin(), m.end(), -1);
        tree.resize(n);
        res.resize(n, 0);
        for (int i = 1; i < n; i++) {
            int p = parent[i];
            tree[p].insert(i);
        }
        dfs(0, parent, s);
        return res;
    }

    void dfs(int idx, vector<int>& parent, string& s) {
        int c = s[idx] - 'a', prev = m[c];
        m[c] = idx;
        res[idx] += 1;
        for (int child : tree[idx]) {
            dfs(child, parent, s);
            int anc = m[s[child] - 'a'];
            res[anc < 0 ? idx : anc] += res[child];
        }
        m[c] = prev;
    }
};

Two DFS:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
class Solution {
public:
    vector<vector<int>> children;
    array<int, 26> m;
    string s_;
    vector<int> res;

    vector<int> findSubtreeSizes(vector<int>& parent, string s) {
        int n = s.size(); s_ = s;
        for (int i = 0; i < 26; i++) {
            m[i] = -1;
        }
        children.resize(n, vector<int>());
        res.resize(n);
        buildTree(parent);
        dfs(0, parent);
        children.clear();
        children.resize(n, vector<int>());
        buildTree(parent);
        dfsCount(0, parent);
        return res;
    }

    int dfsCount(int idx, vector<int>& parent) {
        int ans = 0;
        for (int child : children[idx]) {
            ans += dfsCount(child, parent);
        }
        res[idx] = ans + 1;
        return ans + 1;
    }

    void dfs(int idx, vector<int>& parent) {
        int c = s_[idx] - 'a', prev = -1;
        if (m[c] != -1) {
            parent[idx] = m[c];
            prev = m[c];
        }
        m[c] = idx;
        for (int child : children[idx]) {
            dfs(child, parent);
        }
        m[c] = prev;
    }

    void buildTree(vector<int>& parent) {
        int n = parent.size();
        for (int i = 0; i < parent.size(); i++) {
            if (parent[i] != -1)  {
                int p = parent[i];
                children[p].push_back(i);
            }
        }
    }
};