3327. Check if DFS Strings Are Palindromes

Posted on Edited on In

3327. Check if DFS Strings Are Palindromes

Description

You are given a tree rooted at node 0, consisting of n nodes numbered from 0 to n - 1. The tree is represented by an array parent of size n, where parent[i] is the parent of node i. Since node 0 is the root, parent[0] == -1.

You are also given a string s of length n, where s[i] is the character assigned to node i.

Consider an empty string dfsStr, and define a recursive function dfs(int x) that takes a node x as a parameter and performs the following steps in order:

  • Iterate over each child y of x in increasing order of their numbers , and call dfs(y).
  • Add the character s[x] to the end of the string dfsStr.

Note that dfsStr is shared across all recursive calls of dfs.

You need to find a boolean array answer of size n, where for each index i from 0 to n - 1, you do the following:

  • Empty the string dfsStr and call dfs(i).
  • If the resulting string dfsStr is a palindrome, then set answer[i] to true. Otherwise, set answer[i] to false.

Return the array answer.

Example 1:

1
2
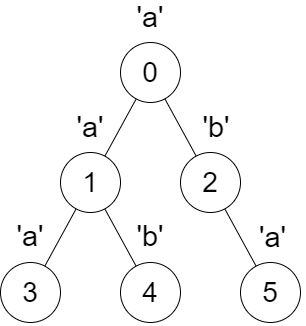
3
Input: parent = [-1,0,0,1,1,2], s = "aababa"

Output: [true,true,false,true,true,true]

Explanation:

  • Calling dfs(0) results in the string dfsStr = "abaaba", which is a palindrome.
  • Calling dfs(1) results in the string dfsStr = "aba", which is a palindrome.
  • Calling dfs(2) results in the string dfsStr = "ab", which is not a palindrome.
  • Calling dfs(3) results in the string dfsStr = "a", which is a palindrome.
  • Calling dfs(4) results in the string dfsStr = "b", which is a palindrome.
  • Calling dfs(5) results in the string dfsStr = "a", which is a palindrome.

Example 2:

1
2
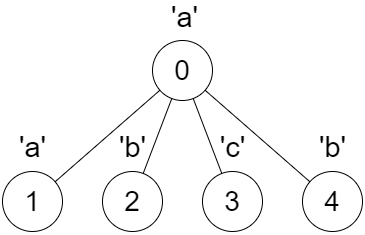
3
Input: parent = [-1,0,0,0,0], s = "aabcb"

Output: [true,true,true,true,true]

Explanation:

Every call on dfs(x) results in a palindrome string.

Constraints:

  • n == parent.length == s.length
  • 1 <= n <= 10^5
  • 0 <= parent[i] <= n - 1 for all i >= 1.
  • parent[0] == -1
  • parent represents a valid tree.
  • s consists only of lowercase English letters.

Hints/Notes

Solution

Language: C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
class Solution {
public:
    vector<set<int>> children;
    vector<pair<int, int>> ranges;
    int cur = 0;
    string s_, postorder;

    vector<bool> findAnswer(vector<int>& parent, string s) {
        int n = s.size();
        s_ = s;
        children.resize(n);
        ranges.resize(n);
        buildTree(parent);
        dfs(0);
        // now we have the full string in postorder, let's manacher
        // step 0: pre-processing the string
        string manacher = "^#";
        for (char c : postorder) {
            manacher.push_back(c);
            manacher.push_back('#');
        }
        manacher.push_back('$');
        // cout << manacher << endl;
        vector<int> halfLen(manacher.size(), 0);
        int center = 0, right = 0;
        for (int i = 1; i < manacher.size() - 1; i++) {
            int len = 0;
            if (i < right) {
                len = min(right - i, halfLen[2 * center - i]);
            }
            while (manacher[i + len] == manacher[i - len]) {
                if (i + len > right) {
                    right = i + len;
                    center = i;
                }
                len++;
            }
            halfLen[i] = len;
        }
        vector<bool> res(n);
        for (int i = 0; i < n; i++) {
            auto duo = ranges[i];
            int l = duo.first * 2 + 2;
            int r = duo.second * 2 + 2;
            res[i] = halfLen[(l + r) / 2] > (r - l) / 2;
        }
        return res;
    }

    void dfs(int u) {
        int l = cur;
        for (int child : children[u]) {
            dfs(child);
        }
        ranges[u] = {l, cur};
        cur++;
        postorder.push_back(s_[u]);
    }

    void buildTree(vector<int>& parent) {
        int n = parent.size();
        for (int i = 0; i < n; i++) {
            int p = parent[i];
            if (p != -1) {
                children[p].insert(i);
            }
        }
    }
};