3311. Construct 2D Grid Matching Graph Layout

Posted on Edited on In

3311. Construct 2D Grid Matching Graph Layout

Description

You are given a 2D integer array edges representing an undirected graph having n nodes, where edges[i] = [ui, vi] denotes an edge between nodes ui and vi.

Construct a 2D grid that satisfies these conditions:

  • The grid contains all nodes from 0 to n - 1 in its cells, with each node appearing exactly once .
  • Two nodes should be in adjacent grid cells (horizontally or vertically ) if and only if there is an edge between them in edges.

It is guaranteed that edges can form a 2D grid that satisfies the conditions.

Return a 2D integer array satisfying the conditions above. If there are multiple solutions, return any of them.

Example 1:

1
2
3
Input: n = 4, edges = [[0,1],[0,2],[1,3],[2,3]]

Output: [[3,1],[2,0]]

Explanation:

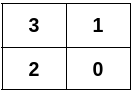
Example 2:

1
2
3
Input: n = 5, edges = [[0,1],[1,3],[2,3],[2,4]]

Output: [[4,2,3,1,0]]

Explanation:

Example 3:

1
2
3
Input: n = 9, edges = [[0,1],[0,4],[0,5],[1,7],[2,3],[2,4],[2,5],[3,6],[4,6],[4,7],[6,8],[7,8]]

Output: [[8,6,3],[7,4,2],[1,0,5]]

Explanation:

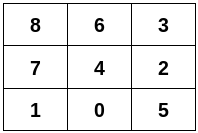
Constraints:

  • 2 <= n <= 5 * 10^4
  • 1 <= edges.length <= 10^5
  • edges[i] = [u<sub>i</sub>, v<sub>i</sub>]
  • 0 <= u<sub>i</sub> < v<sub>i</sub> < n
  • All the edges are distinct.
  • The input is generated such that edges can form a 2D grid that satisfies the conditions.

Hints/Notes

Solution

Language: C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
class Solution {
public:
    vector<vector<int>> constructGridLayout(int n, vector<vector<int>>& edges) {
        unordered_map<int, vector<int>> m;
        vector<vector<int>> graph(n);
        for (auto edge : edges) {
            int u = edge[0];
            int v = edge[1];
            graph[u].push_back(v);
            graph[v].push_back(u);
        }
        for (int i = 0; i < n; i++) {
            int degree = graph[i].size();
            m[degree].push_back(i);
        }
        vector<int> first_row;
        vector<bool> visited(n, false);
        // there are at least 3 columns
        if (m.contains(4)) {
            int u = m[2].front();
            visited[u] = true;
            first_row.push_back(u);
            u = graph[u][0];
            while (graph[u].size() > 2) {
                visited[u] = true;
                first_row.push_back(u);
                for (int v : graph[u]) {
                    if (graph[v].size() < 4 && !visited[v]) {
                        u = v;
                        break;
                    }
                }
            }
            first_row.push_back(u);
            visited[u] = true;
            // there is only 1 columns
        } else if (m.contains(1)) {
            int u = m[1].front();
            visited[u] = true;
            first_row.push_back(u);
        } else {
            int u = m[2].front();
            visited[u] = true;
            first_row.push_back(u);
            for (int v : graph[u]) {
                if (graph[v].size() == 2) {
                    first_row.push_back(v);
                    visited[v] = true;
                    break;
                }
            }
        }
        vector<vector<int>> res;
        res.push_back(first_row);
        for (int i = 1; i < n / (int)first_row.size(); i++) {
            vector<int> next_row;
            for (int u : first_row) {
                for (int v : graph[u]) {
                    if (!visited[v]) {
                        visited[v] = true;
                        next_row.push_back(v);
                        break;
                    }
                }
            }
            res.push_back(next_row);
            first_row = next_row;
        }
        return res;
    }
};