3235. Check if the Rectangle Corner Is Reachable

Posted on Edited on In

3235. Check if the Rectangle Corner Is Reachable

Description

You are given two positive integers xCorner and yCorner, and a 2D array circles, where circles[i] = [xi, yi, ri] denotes a circle with center at (xi, yi) and radius ri.

There is a rectangle in the coordinate plane with its bottom left corner at the origin and top right corner at the coordinate (xCorner, yCorner). You need to check whether there is a path from the bottom left corner to the top right corner such that the entire path lies inside the rectangle, does not touch or lie inside any circle, and touches the rectangle only at the two corners.

Return true if such a path exists, and false otherwise.

Example 1:

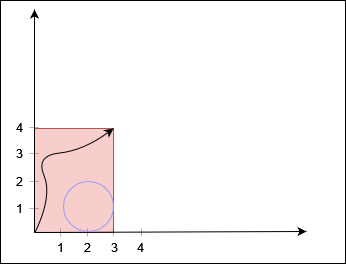
1
2
3
Input: xCorner = 3, yCorner = 4, circles = [[2,1,1]]

Output: true

Explanation:

The black curve shows a possible path between (0, 0) and (3, 4).

Example 2:

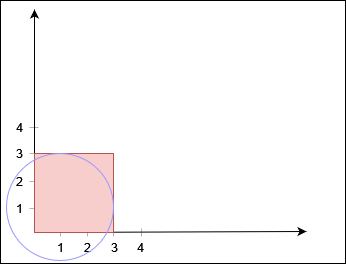
1
2
3
Input: xCorner = 3, yCorner = 3, circles = [[1,1,2]]

Output: false

Explanation:

No path exists from (0, 0) to (3, 3).

Example 3:

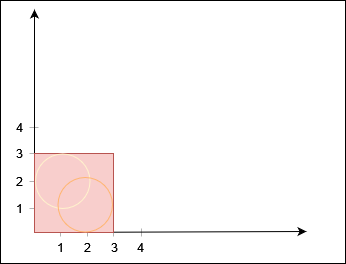
1
2
3
Input: xCorner = 3, yCorner = 3, circles = [[2,1,1],[1,2,1]]

Output: false

Explanation:

No path exists from (0, 0) to (3, 3).

Example 4:

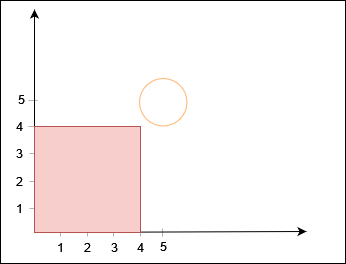
1
2
3
Input: xCorner = 4, yCorner = 4, circles = [[5,5,1]]

Output: true

Explanation:

Constraints:

  • 3 <= xCorner, yCorner <= 10^9
  • 1 <= circles.length <= 1000
  • circles[i].length == 3
  • 1 <= xi, yi, ri <= 10^9

Hints/Notes

  • union find
  • Weekly Contest 408

Solution

Language: C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
class Solution {
public:
    vector<int> nodes;

    bool canReachCorner(int xCorner, int yCorner,
                        vector<vector<int>>& circles) {
        int n = circles.size();
        for (int i = 0; i < n + 2; i++) {
            nodes.push_back(i);
        }
        // the left and up side is n, the right and down side is n + 1
        for (int i = 0; i < n; i++) {
            long x1 = circles[i][0], y1 = circles[i][1], r1 = circles[i][2];
            for (int j = i + 1; j < n; j++) {
                long x2 = circles[j][0], y2 = circles[j][1], r2 = circles[j][2];
                // in this case, the two circle intersects
                if ((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2) <=
                    (r1 + r2) * (r1 + r2)) {
                    // check one point, if it's within the rectangle
                    if (x2 * r1 + x1 * r2 < (r1 + r2) * xCorner &&
                        y2 * r1 + y1 * r2 < (r1 + r2) * yCorner) {
                        merge(i, j);
                    }
                }
            }
            bool leftUp = inCircle(0, yCorner, x1, y1, r1);
            bool rightDown = inCircle(xCorner, 0, x1, y1, r1);
            bool rightUp = inCircle(xCorner, yCorner, x1, y1, r1);
            // the circles are solid, so if it covers all one side, then there's
            // no way to reach the destination
            if ((y1 <= yCorner && x1 <= r1) || (y1 > yCorner && leftUp)) {
                merge(i, n);
            }
            if ((x1 <= xCorner && abs(y1 - yCorner) <= r1) ||
                (x1 > xCorner && rightUp)) {
                merge(i, n);
            }
            if ((y1 <= yCorner && abs(x1 - xCorner) <= r1) ||
                (y1 > yCorner && rightUp)) {
                merge(i, n + 1);
            }
            if ((x1 <= xCorner && y1 <= r1) || (y1 > yCorner && rightDown)) {
                merge(i, n + 1);
            }
            if (find(n) == find(n + 1)) {
                return false;
            }
        }
        return true;
    }

    void merge(int u, int v) {
        int rootU = find(u), rootV = find(v);
        nodes[rootU] = rootV;
    }

    int find(int u) {
        while (nodes[u] != u) {
            nodes[u] = find(nodes[u]);
            u = nodes[u];
        }
        return u;
    }

    bool inCircle(long x0, long y0, long x1, long y1, long r) {
        return (x0 - x1) * (x0 - x1) + (y0 - y1) * (y0 - y1) <= r * r;
    }
};