3240. Minimum Number of Flips to Make Binary Grid Palindromic II

Posted on Edited on In

3240. Minimum Number of Flips to Make Binary Grid Palindromic II

Description

You are given an m x n binary matrix grid.

A row or column is considered palindromic if its values read the same forward and backward.

You can flip any number of cells in grid from 0 to 1, or from 1 to 0.

Return the minimum number of cells that need to be flipped to make all rows and columns palindromic , and the total number of 1‘s in grid divisible by 4.

Example 1:

1
2
3
Input: grid = [[1,0,0],[0,1,0],[0,0,1]]

Output: 3

Explanation:

Example 2:

1
2
3
Input: grid = [[0,1],[0,1],[0,0]]

Output: 2

Explanation:

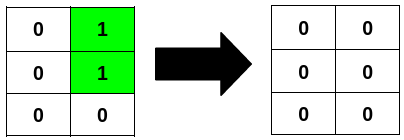
Example 3:

1
2
3
Input: grid = [[1],[1]]

Output: 2

Explanation:

Constraints:

  • m == grid.length
  • n == grid[i].length
  • 1 <= m * n <= 2 * 10^5
  • 0 <= grid[i][j] <= 1

Hints/Notes

Solution

Language: C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
class Solution {
public:
    int minFlips(vector<vector<int>>& grid) {
        int res = 0, m = grid.size(), n = grid[0].size();
        for (int i = 0; i < m / 2; i++) {
            for (int j = 0; j < n / 2; j++) {
                int tmp = grid[i][j] + grid[m - 1 - i][j] + grid[i][n - 1 - j] +
                          grid[m - 1 - i][n - 1 - j];
                res += min(tmp, 4 - tmp);
            }
        }
        // the center point must be zero
        if (m % 2 && n % 2) {
            res += grid[m / 2][n / 2];
        }

        // for the middle row and middle col, we sum
        // 1. the number of 1s when the numbers are the same
        // 2. the number of diff
        //
        // 1. if the number of 1s is divisible by 4, then we only
        // need to add diff, which means make all 1 zero
        // 2. if the number of 1s divide 4 == 2, then if we have diff
        // we can make 1 pair of diff to 1, otherwise, we need diff + 2
        int count = 0, diff = 0;
        if (m % 2) {
            for (int i = 0; i < n / 2; i++) {
                if (grid[m / 2][i] != grid[m / 2][n - 1 - i]) {
                    diff++;
                } else {
                    count += 2 * grid[m / 2][i];
                }
            }
        }
        if (n % 2) {
            for (int i = 0; i < m / 2; i++) {
                if (grid[i][n / 2] != grid[m - 1 - i][n / 2]) {
                    diff++;
                } else {
                    count += 2 * grid[i][n / 2];
                }
            }
        }

        if (count % 4 == 0) {
            res += diff;
        } else if (count % 4 == 2) {
            if (diff > 0) {
                res += diff;
            } else {
                res += 2;
            }
        }
        return res;
    }
};