931. Minimum Falling Path Sum

Posted on Edited on In

931. Minimum Falling Path Sum

Description

Given an n x n array of integers matrix, return the minimum sum of any falling path through matrix.

A falling path starts at any element in the first row and chooses the element in the next row that is either directly below or diagonally left/right. Specifically, the next element from position (row, col) will be (row + 1, col - 1), (row + 1, col), or (row + 1, col + 1).

Example 1:

1
2
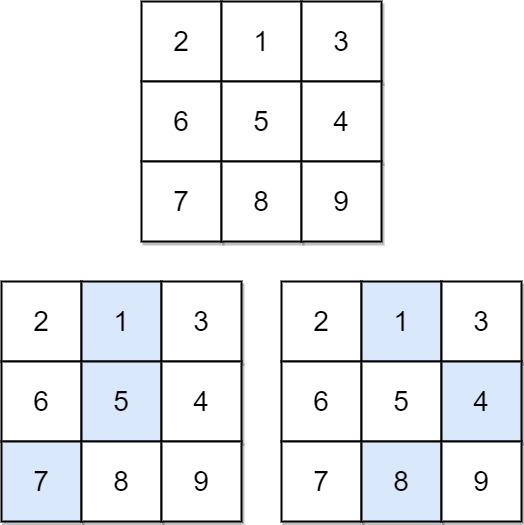
3
Input: matrix = [[2,1,3],[6,5,4],[7,8,9]]
Output: 13
Explanation: There are two falling paths with a minimum sum as shown.

Example 2:

1
2
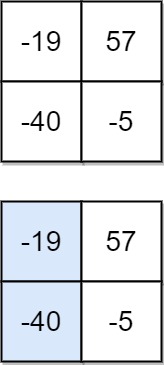
3
Input: matrix = [[-19,57],[-40,-5]]
Output: -59
Explanation: The falling path with a minimum sum is shown.

Constraints:

  • n == matrix.length == matrix[i].length
  • 1 <= n <= 100
  • -100 <= matrix[i][j] <= 100

Hints/Notes

Solution

Language: C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    vector<vector<int>> dp;

    int minFallingPathSum(vector<vector<int>>& matrix) {
        int m = matrix.size(), n = matrix[0].size();
        dp.resize(m, vector<int>(n, INT_MAX));
        int minVal = INT_MAX;
        for (int i = 0; i < n; i++) {
            dp[0][i] = matrix[0][i];
            minVal = min(minVal, dp[0][i]);
        }
        for (int i = 1; i < m; i++) {
            minVal = INT_MAX;
            for (int j = 0; j < n; j++) {
                int v1 = j ? dp[i - 1][j - 1] : INT_MAX;
                int v2 = dp[i - 1][j];
                int v3 = j == n - 1 ? INT_MAX : dp[i - 1][j + 1];
                dp[i][j] = matrix[i][j] + min(v1, min(v2, v3));
                minVal = min(minVal, dp[i][j]);
            }
        }
        return minVal;
    }
};