3208. Alternating Groups II

Posted on Edited on In

3208. Alternating Groups II

Description

There is a circle of red and blue tiles. You are given an array of integers colors and an integer k. The color of tile i is represented by colors[i]:

  • colors[i] == 0 means that tile i is red .
  • colors[i] == 1 means that tile i is blue .

An alternating group is every k contiguous tiles in the circle with alternating colors (each tile in the group except the first and last one has a different color from its left and right tiles).

Return the number of alternating groups.

Note that since colors represents a circle , the first and the last tiles are considered to be next to each other.

Example 1:

1
2
3
Input: colors = [0,1,0,1,0], k = 3

Output: 3

Explanation:

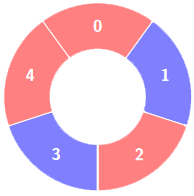
Alternating groups:

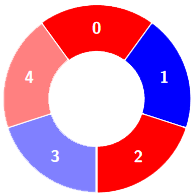
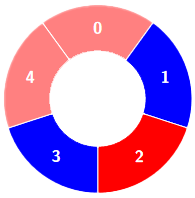
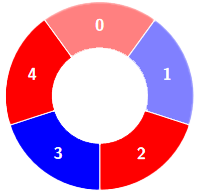
Example 2:

1
2
3
Input: colors = [0,1,0,0,1,0,1], k = 6

Output: 2

Explanation:

Alternating groups:

Example 3:

1
2
3
Input: colors = [1,1,0,1], k = 4

Output: 0

Explanation:

Constraints:

  • 3 <= colors.length <= 10^5
  • 0 <= colors[i] <= 1
  • 3 <= k <= colors.length

Hints/Notes

  • sliding window
  • Biweekly Contest 134

Solution

Language: C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int numberOfAlternatingGroups(vector<int>& colors, int k) {
        int n = colors.size();
        int cur = colors[0], curLength = 1, res = 0;
        for (int i = 1; i < n + k; i++) {
            if (colors[i % n] != cur) {
                curLength++;
                cur = 1 - cur;
            } else {
                res += max(0, curLength - k + 1);
                cur = colors[i % n];
                curLength = 1;
            }
        }
        res += max(0, curLength - k);
        return res;
    }
};