979. Distribute Coins in Binary Tree

Posted on Edited on In

979. Distribute Coins in Binary Tree

Description

You are given the root of a binary tree with n nodes where each node in the tree has node.val coins. There are n coins in total throughout the whole tree.

In one move, we may choose two adjacent nodes and move one coin from one node to another. A move may be from parent to child, or from child to parent.

Return the minimum number of moves required to make every node have exactly one coin.

Example 1:

1
2
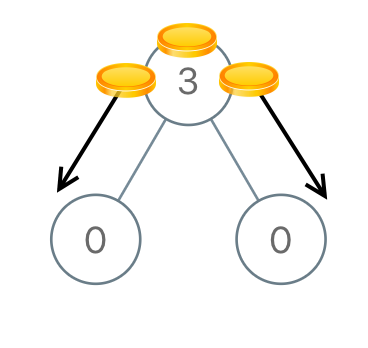
3
Input: root = [3,0,0]
Output: 2
Explanation: From the root of the tree, we move one coin to its left child, and one coin to its right child.

Example 2:

1
2
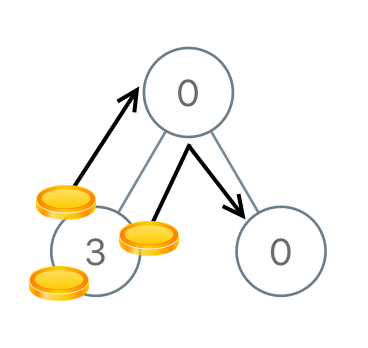
3
Input: root = [0,3,0]
Output: 3
Explanation: From the left child of the root, we move two coins to the root [taking two moves]. Then, we move one coin from the root of the tree to the right child.

Constraints:

  • The number of nodes in the tree is n.
  • 1 <= n <= 100
  • 0 <= Node.val <= n
  • The sum of all Node.val is n.

Hints/Notes

  • binary tree

Solution

Language: C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),
 * right(right) {}
 * };
 */
class Solution {
public:
    int ans = 0;

    int distributeCoins(TreeNode* root) {
        traverse(root, 0);
        return ans;
    }

    int traverse(TreeNode* root) {
        if (!root) {
            return 0;
        }

        int l = traverse(root->left);
        int r = traverse(root->right);

        // try to understand this bottom up, so we return the excess
        // coins back to parent, and rem here is the number of coins
        // we need to transfer away
        int rem = l + r + root->val - 1;
        ans += abs(rem);
        return rem;
    }
};