3203. Find Minimum Diameter After Merging Two Trees

Posted on Edited on In

3203. Find Minimum Diameter After Merging Two Trees

Description

There exist two undirected trees with n and m nodes, numbered from 0 to n - 1 and from 0 to m - 1, respectively. You are given two 2D integer arrays edges1 and edges2 of lengths n - 1 and m - 1, respectively, where edges1[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the first tree and edges2[i] = [ui, vi] indicates that there is an edge between nodes ui and vi in the second tree.

You must connect one node from the first tree with another node from the second tree with an edge.

Return the minimum possible diameter of the resulting tree.

The diameter of a tree is the length of the longest path between any two nodes in the tree.

Example 1:

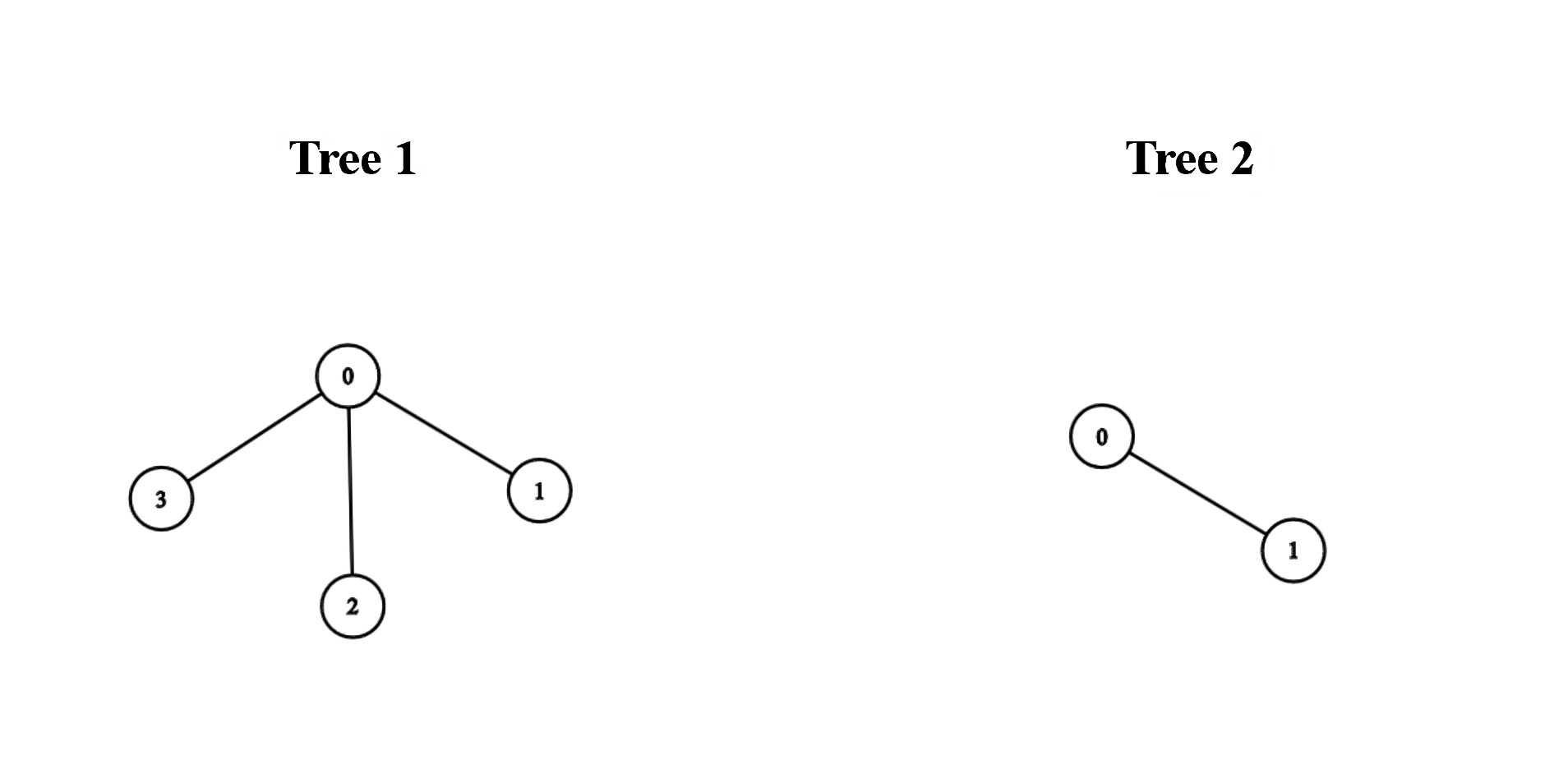
1
2
3
4
5
6
7
Input: edges1 = [[0,1],[0,2],[0,3]], edges2 = [[0,1]]

Output: 3

Explanation:

We can obtain a tree of diameter 3 by connecting node 0 from the first tree with any node from the second tree.

Example 2:

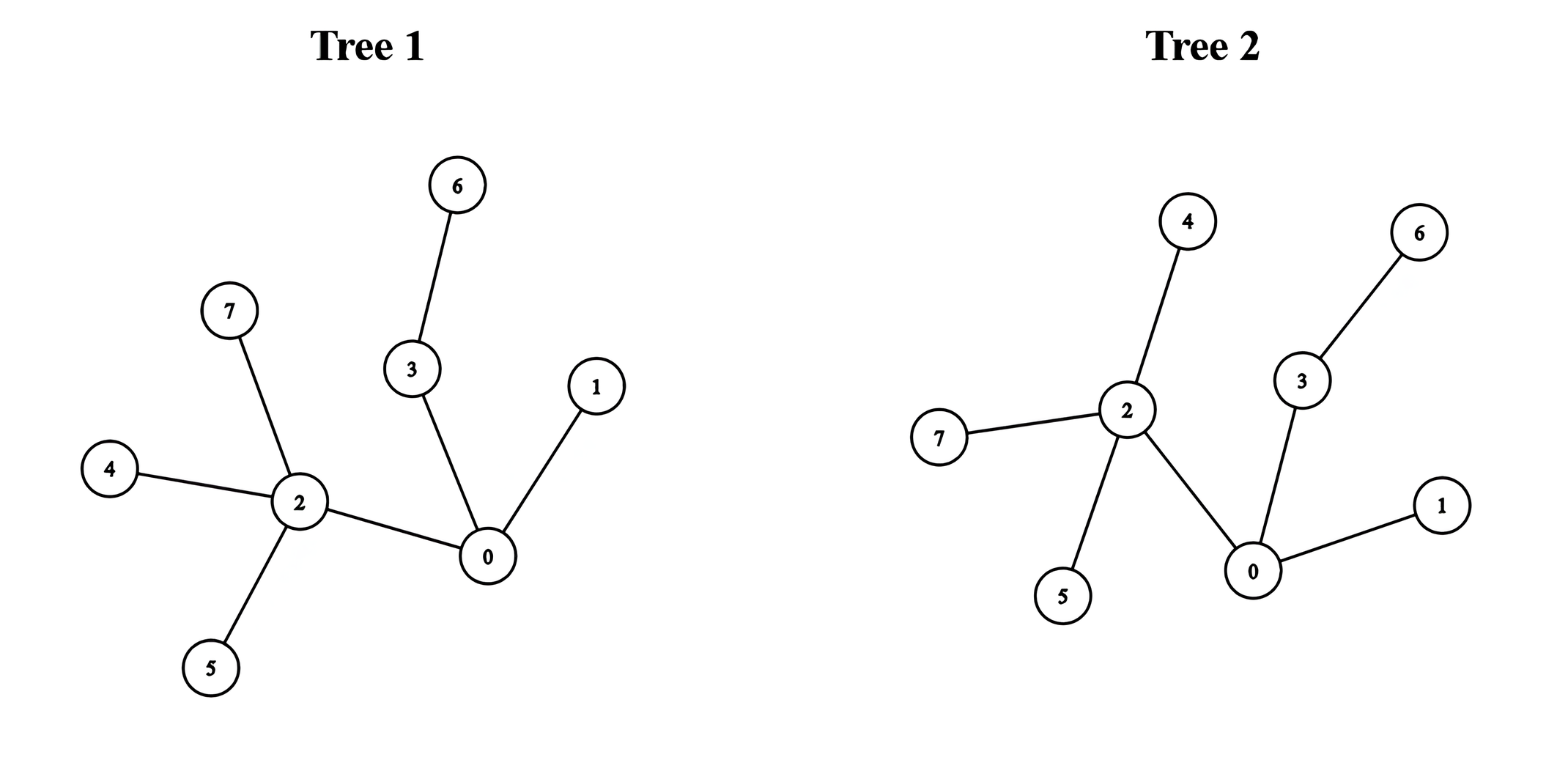
1
2
3
4
5
6
7
Input: edges1 = [[0,1],[0,2],[0,3],[2,4],[2,5],[3,6],[2,7]], edges2 = [[0,1],[0,2],[0,3],[2,4],[2,5],[3,6],[2,7]]

Output: 5

Explanation:

We can obtain a tree of diameter 5 by connecting node 0 from the first tree with node 0 from the second tree.

Constraints:

  • 1 <= n, m <= 10^5
  • edges1.length == n - 1
  • edges2.length == m - 1
  • edges1[i].length == edges2[i].length == 2
  • edges1[i] = [ai, bi]
  • 0 <= ai, bi < n
  • edges2[i] = [ui, vi]
  • 0 <= ui, vi < m
  • The input is generated such that edges1 and edges2 represent valid trees.

Hints/Notes

  • Tree dp
  • Weekly Contest 404

Solution

Language: C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
class Solution {
public:
    int minimumDiameterAfterMerge(vector<vector<int>>& edges1, vector<vector<int>>& edges2) {
        int selfD1, selfD2;
        int d1 = findRoot(edges1, selfD1);
        int d2 = findRoot(edges2, selfD2);
        // cout << d1 << " " << d2 << " " << selfD1 << " " << selfD2 << endl;
        return max(d1 + d2 + 1, max(selfD1, selfD2));
    }

    int findRoot(vector<vector<int>>& edges, int& self) {
        if (edges.empty()) {
            self = 0;
            return 0;
        }
        self = 0;
        int size = edges.size() + 1;
        vector<vector<int>> tree(size, vector<int>());
        unordered_map<int, int> m;
        for (auto edge : edges) {
            int u = edge[0];
            int v = edge[1];
            tree[u].push_back(v);
            tree[v].push_back(u);
            m[u]++;
            m[v]++;
        }
        unordered_set<int> visited;
        queue<int> q;
        for (int i = 0; i < size; i++) {
            if (m[i] == 1) {
                visited.insert(i);
                m[i]--;
                q.push(i);
            }
        }
        int d = 1;
        while (!q.empty()) {
            int size = q.size();
            for (int i = 0; i < size; i++) {
                int u = q.front();
                q.pop();
                for (int num : tree[u]) {
                    m[num]--;
                    if (!visited.contains(num) && m[num] == 1) {
                        visited.insert(num);
                        m[num]--;
                        q.push(num);
                    }
                }
            }
            if (q.size() > 1) {
                d++;
                self += 2;
            } else {
                self += 1;
            }
        }
        return d;
    }
};

Another approach: Tree DP

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution {
public:
    int res;

    int minimumDiameterAfterMerge(vector<vector<int>>& edges1, vector<vector<int>>& edges2) {
        int selfD1, selfD2;
        int d1 = diameter(edges1);
        int d2 = diameter(edges2);
        // cout << d1 << " " << d2 << " " << endl;
        return max((d1 + 1) / 2 + (d2 + 1) / 2 + 1, max(d1, d2));
    }

    int diameter(vector<vector<int>>& edges) {
        if (edges.empty()) {
            return 0;
        }
        int size = edges.size() + 1;
        vector<vector<int>> tree(size, vector<int>());
        for (auto edge : edges) {
            int u = edge[0];
            int v = edge[1];
            tree[u].push_back(v);
            tree[v].push_back(u);
        }
        res = 0;
        dfs(0, -1, tree);
        return res;
    }



    int dfs(int cur, int prev, vector<vector<int>>& tree) {
        int mx1 = 0, mx2 = 0;
        for (int v : tree[cur]) {
            if (v != prev) {
                int tmp = dfs(v, cur, tree);
                if (tmp > mx1) {
                    mx2 = mx1;
                    mx1 = tmp;
                } else if (tmp > mx2) {
                    mx2 = tmp;
                }
            }
        }
        res = max(res, mx1 + mx2);
        return max(mx1, mx2) + 1;
    }
};