1026. Maximum Difference Between Node and Ancestor

Posted on Edited on In

1026. Maximum Difference Between Node and Ancestor

Description

Given the root of a binary tree, find the maximum value v for which there exist different nodes a and b where v = |a.val - b.val| and a is an ancestor of b.

A node a is an ancestor of b if either: any child of a is equal to bor any child of a is an ancestor of b.

Example 1:

1
2
3
4
5
6
7
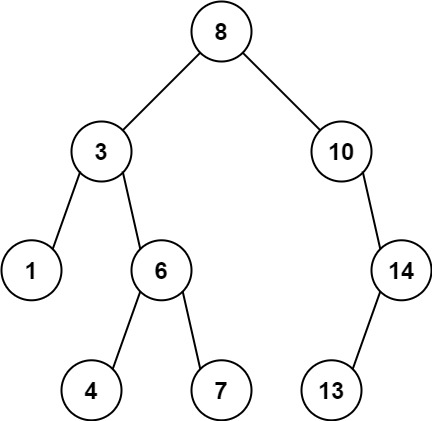
8
Input: root = [8,3,10,1,6,null,14,null,null,4,7,13]
Output: 7
Explanation: We have various ancestor-node differences, some of which are given below :
|8 - 3| = 5
|3 - 7| = 4
|8 - 1| = 7
|10 - 13| = 3
Among all possible differences, the maximum value of 7 is obtained by |8 - 1| = 7.

Example 2:

1
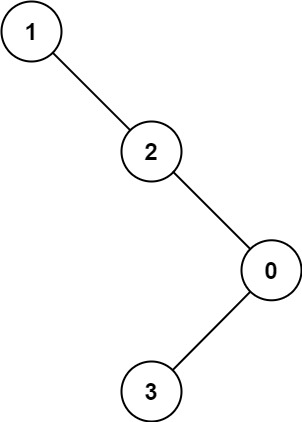
2
Input: root = [1,null,2,null,0,3]
Output: 3

Constraints:

  • The number of nodes in the tree is in the range [2, 5000].
  • 0 <= Node.val <= 10^5

Hints/Notes

  • back tracking

Solution

Language: C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),
 * right(right) {}
 * };
 */
class Solution {
public:
    map<int, int> s;
    int res = 0;

    int maxAncestorDiff(TreeNode* root) {
        traverse(root);
        return res;
    }

    void traverse(TreeNode* root) {
        if (!root) {
            return;
        }
        s[root->val]++;
        int minVal = s.begin()->first;
        int maxVal = s.rbegin()->first;
        res = max(res, abs(maxVal - minVal));
        traverse(root->left);
        traverse(root->right);
        s[root->val]--;
        if (s[root->val] == 0) {
            s.erase(root->val);
        }
    }
};