894. All Possible Full Binary Trees
894. All Possible Full Binary Trees
Description
Given an integer n, return a list of all possible full binary trees with n nodes. Each node of each tree in the answer must have Node.val == 0.
Each element of the answer is the root node of one possible tree. You may return the final list of trees in any order .
A full binary tree is a binary tree where each node has exactly 0 or 2 children.
Example 1: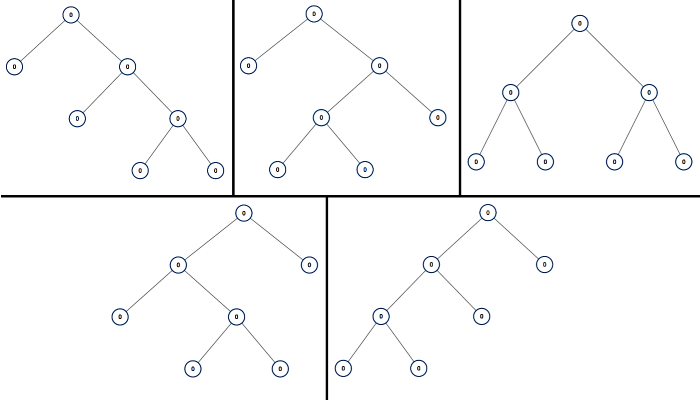
1 | Input: n = 7 |
Example 2:
1 | Input: n = 3 |
Constraints:
1 <= n <= 20
Hints/Notes
- N/A
Solution
Language: C++
1 | /** |