3149. Find the Minimum Cost Array Permutation

Posted on Edited on In

3149. Find the Minimum Cost Array Permutation

Description

You are given an array nums which is a permutation of [0, 1, 2, ..., n - 1]. The score of any permutation of [0, 1, 2, ..., n - 1] named perm is defined as:

score(perm) = |perm[0] - nums[perm[1]]| + |perm[1] - nums[perm[2]]| + ... + |perm[n - 1] - nums[perm[0]]|

Return the permutation perm which has the minimum possible score. If multiple permutations exist with this score, return the one that is lexicographically smallest among them.

Example 1:

1
2
3
Input: nums = [1,0,2]

Output: [0,1,2]

Explanation:

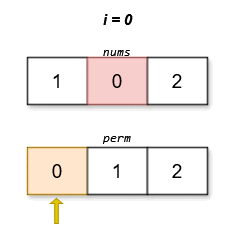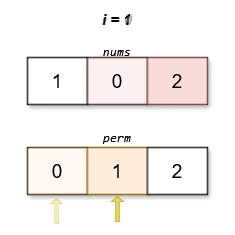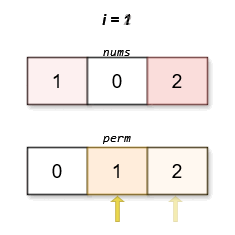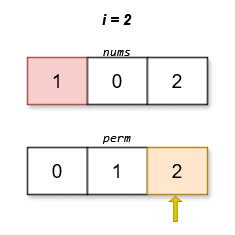
The lexicographically smallest permutation with minimum cost is [0,1,2]. The cost of this permutation is |0 - 0| + |1 - 2| + |2 - 1| = 2.

Example 2:

1
2
3
Input: nums = [0,2,1]

Output: [0,2,1]

Explanation:

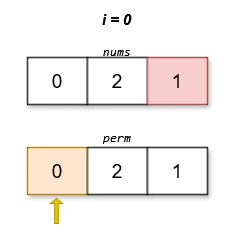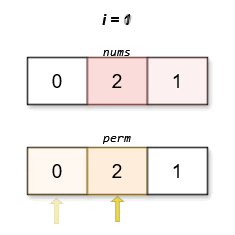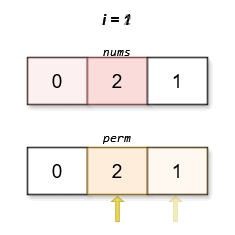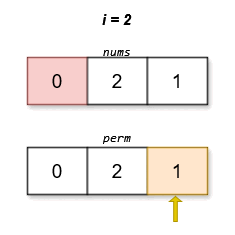
The lexicographically smallest permutation with minimum cost is [0,2,1]. The cost of this permutation is |0 - 1| + |2 - 2| + |1 - 0| = 2.

Constraints:

  • 2 <= n == nums.length <= 14
  • nums is a permutation of [0, 1, 2, ..., n - 1].

Hints/Notes

  • Weekly contest 397
  • Rotate the array we can get the same result, so always start with zero
  • Think about how to transition from one state to next

Solution

Language: C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution {
public:
    int size_;
    vector<int> res;

    vector<int> findPermutation(vector<int>& nums) {
        size_ = nums.size();
        vector<vector<long>> dp((1 << size_) - 1, vector<long>(nums.size(), INT_MAX));
        dfs(1, 0, dp, nums);
        make_ans(1, 0, dp, nums);
        return res;
    }

    int dfs(long i, int j, vector<vector<long>>& dp, vector<int>& nums) {
        if (i == (1 << size_) - 1) {
            return abs(j - nums[0]);
        }
        if (dp[i][j] != INT_MAX) {
            return dp[i][j];
        }
        int res = INT_MAX;
        for (int k = 0; k < size_; k++) {
            if ((1 << k) & i) {
                continue;
            }
            res = min(res, abs(j - nums[k]) + dfs(i | (1 << k), k, dp, nums));
        }
        dp[i][j] = res;
        return res;
    }

    void make_ans(long i, int j, vector<vector<long>>& dp, vector<int>& nums) {
        res.push_back(j);
        if (i == (1 << size_) - 1) {
            return;
        }
        for (int k = 0; k < size_; k++) {
            if (i & (1 << k)) {
                continue;
            }
            if (dfs(i | 1 << k, k, dp, nums) + abs(j - nums[k]) == dp[i][j]) {
                make_ans(i | (1 << k), k, dp, nums);
                break;
            }
        }
    }
};