3148. Maximum Difference Score in a Grid

Posted on Edited on In

3148. Maximum Difference Score in a Grid

Description

You are given an m x n matrix grid consisting of positive integers. You can move from a cell in the matrix to any other cell that is either to the bottom or to the right (not necessarily adjacent). The score of a move from a cell with the value c1 to a cell with the value c2 is c2 - c1.

You can start at any cell, and you have to make at least one move.

Return the maximum total score you can achieve.

Example 1:

1
2
3
4
5
6
7
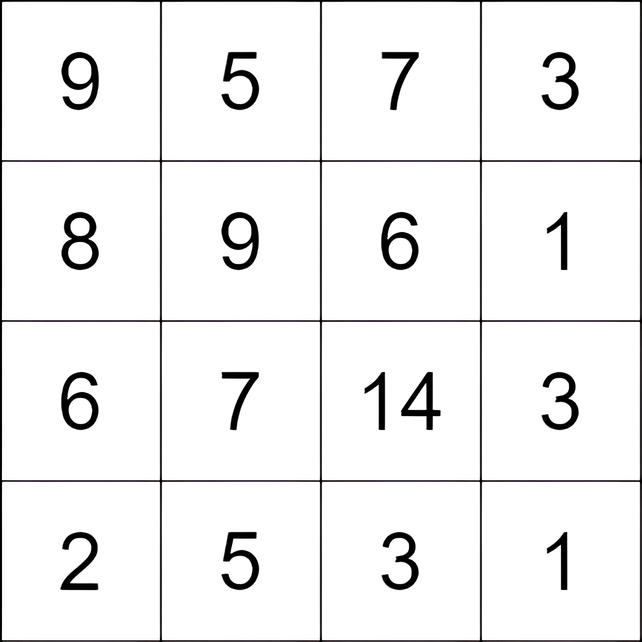
8
Input: grid = [[9,5,7,3],[8,9,6,1],[6,7,14,3],[2,5,3,1]]

Output: 9

Explanation: We start at the cell `(0, 1)`, and we perform the following moves:<br>
- Move from the cell `(0, 1)` to `(2, 1)` with a score of `7 - 5 = 2`.<br>
- Move from the cell `(2, 1)` to `(2, 2)` with a score of `14 - 7 = 7`.<br>
The total score is `2 + 7 = 9`.

Example 2:

1
2
3
4
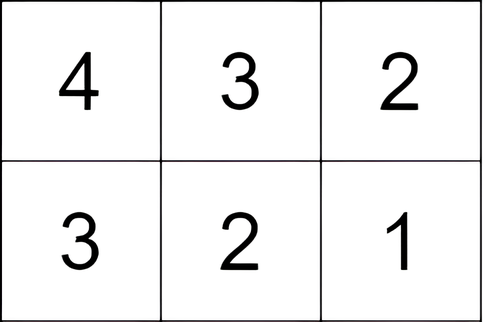
5
Input: grid = [[4,3,2],[3,2,1]]

Output: -1

Explanation: We start at the cell `(0, 0)`, and we perform one move: `(0, 0)` to `(0, 1)`. The score is `3 - 4 = -1`.

Constraints:

  • m == grid.length
  • n == grid[i].length
  • 2 <= m, n <= 1000
  • 4 <= m * n <= 10^5
  • 1 <= grid[i][j] <= 10^5

Hints/Notes

  • Weekly contest 397
  • Calculate prevMin is like 2D preSum

Solution

Language: C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int maxScore(vector<vector<int>>& grid) {
        vector<vector<int>> minNum(grid.size() + 1, vector<int>(grid[0].size() + 1, INT_MAX));
        int res = INT_MIN;
        for (int i = 0; i < grid.size(); i++) {
            for (int j = 0; j < grid[0].size(); j++) {
                int prevMin = min(minNum[i][j + 1], minNum[i + 1][j]);
                res = max(res, grid[i][j] - prevMin);
                minNum[i + 1][j + 1] = min(grid[i][j], prevMin);
            }
        }
        return res;
    }
};