3123. Find Edges in Shortest Paths

Posted on Edited on In

3123. Find Edges in Shortest Paths

Description

You are given an undirected weighted graph of n nodes numbered from 0 to n - 1. The graph consists of m edges represented by a 2D array edges, where edges[i] = [ai, bi, wi] indicates that there is an edge between nodes ai and bi with weight wi.

Consider all the shortest paths from node 0 to node n - 1 in the graph. You need to find a boolean array answer where answer[i] is true if the edge edges[i] is part of at least one shortest path. Otherwise, answer[i] is false.

Return the array answer.

Note that the graph may not be connected.

Example 1:

1
2
3
4
5
6
7
8
9
10
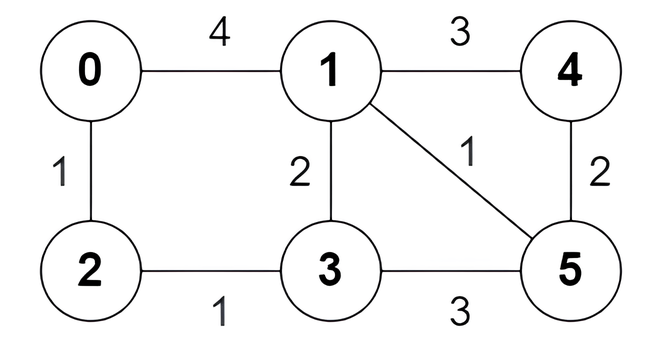
11
Input: n = 6, edges = [[0,1,4],[0,2,1],[1,3,2],[1,4,3],[1,5,1],[2,3,1],[3,5,3],[4,5,2]]

Output: [true,true,true,false,true,true,true,false]

Explanation:

The following are **all**  the shortest paths between nodes 0 and 5:

- The path `0 -> 1 -> 5`: The sum of weights is `4 + 1 = 5`.
- The path `0 -> 2 -> 3 -> 5`: The sum of weights is `1 + 1 + 3 = 5`.
- The path `0 -> 2 -> 3 -> 1 -> 5`: The sum of weights is `1 + 1 + 2 + 1 = 5`.

Example 2:

1
2
3
4
5
6
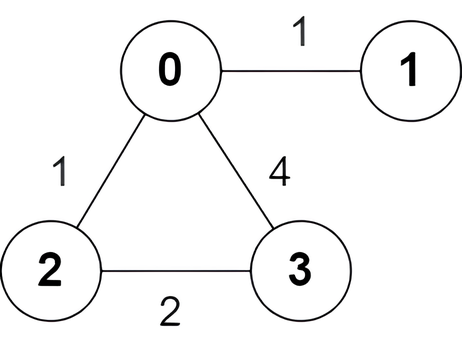
7
Input: n = 4, edges = [[2,0,1],[0,1,1],[0,3,4],[3,2,2]]

Output: [true,false,false,true]

Explanation:

There is one shortest path between nodes 0 and 3, which is the path `0 -> 2 -> 3` with the sum of weights `1 + 2 = 3`.

Constraints:

  • 2 <= n <= 5 * 10^4
  • m == edges.length
  • 1 <= m <= min(5 * 10^4, n * (n - 1) / 2)
  • 0 <= ai, bi < n
  • ai != bi
  • 1 <= wi <= 10^5
  • There are no repeated edges.

Hints/Notes

  • use dijkstra’s algorithm to find the minimum cost to get to each point, then use dfs/bfs to get to all points

Solution

Language: C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
class Solution {
public:
    priority_queue<vector<int>, vector<vector<int>>, greater<vector<int>>> pq;

    vector<bool> findAnswer(int n, vector<vector<int>>& edges) {
        vector<vector<vector<int>>> graph(n, vector<vector<int>>());
        buildGraph(graph, edges);
        vector<bool> res(edges.size(), false);
        vector<int> fromRoot(n, INT_MAX);
        fromRoot[0] = 0;
        pq.push({0, 0});
        while (!pq.empty()) {
            auto e = pq.top();
            pq.pop();
            int u = e[0];
            int w = e[1];
            if (fromRoot[u] < w) {
                continue;
            }
            fromRoot[u] = w;
            for (auto edge : graph[u]) {
                int v = edge[0];
                int weight = edge[1];
                if (fromRoot[v] > w + weight) {
                    fromRoot[v] = w + weight;
                    pq.push({v, w + weight});
                }
            }
        }

        queue<int> q;
        vector<bool> visited(n - 1, false);
        q.push(n - 1);
        while (!q.empty()) {
            int u = q.front();
            q.pop();
            if (visited[u]) {
                continue;
            }
            visited[u] = true;
            for (auto edge : graph[u]) {
                int v = edge[0];
                int weight = edge[1];
                int index = edge[2];
                if (fromRoot[v] == INT_MAX) {
                    continue;
                }
                if (fromRoot[v] + weight == fromRoot[u]) {
                    res[index] = true;
                    q.push(v);
                }
            }
        }
        return res;
    }

    void buildGraph(vector<vector<vector<int>>>& graph, vector<vector<int>>& edges) {
        for (int i = 0; i < edges.size(); i++) {
            auto edge = edges[i];
            int u = edge[0];
            int v = edge[1];
            int w = edge[2];
            graph[u].push_back({v, w, i});
            graph[v].push_back({u, w, i});
        }
    }
};