3122. Minimum Number of Operations to Satisfy Conditions

Posted on Edited on In

3122. Minimum Number of Operations to Satisfy Conditions

Description

You are given a 2D matrix grid of size m x n. In one operation , you can change the value of any cell to any non-negative number. You need to perform some operations such that each cell grid[i][j] is:

  • Equal to the cell below it, i.e. grid[i][j] == grid[i + 1][j] (if it exists).
  • Different from the cell to its right, i.e. grid[i][j] != grid[i][j + 1] (if it exists).

Return the minimum number of operations needed.

Example 1:

1
2
3
Input: grid = [[1,0,2],[1,0,2]]

Output: 0

Explanation:

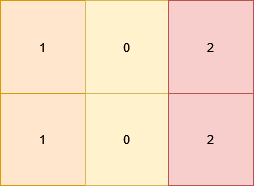
All the cells in the matrix already satisfy the properties.

Example 2:

1
2
3
Input: grid = [[1,1,1],[0,0,0]]

Output: 3

Explanation:

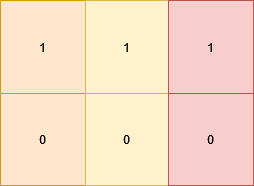
The matrix becomes [[1,0,1],[1,0,1]] which satisfies the properties, by doing these 3 operations:

  • Change grid[1][0] to 1.
  • Change grid[0][1] to 0.
  • Change grid[1][2] to 1.

Example 3:

1
2
3
Input: grid = [[1],[2],[3]]

Output: 2

Explanation:

There is a single column. We can change the value to 1 in each cell using 2 operations.

Constraints:

  • 1 <= n, m <= 1000
  • 0 <= grid[i][j] <= 9

Hints/Notes

  • we can use the previous column’s color, and the best sol + second_best sol to get the current column’s best sol and second_best sol

Solution

Language: C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    int minimumOperations(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        int f0 = 0, f1 = 0, pre = -1;
        for (int j = 0; j < n; j++) {
            vector<int> count(10, 0);
            for (int i = 0; i < m; i++) {
                count[grid[i][j]]++;
            }
            // count[0] = 1
            // count[1] = 1
            int min1 = INT_MAX, min2 = INT_MAX, curMin = -1;
            for (int i = 0; i < 10; i++) {
                count[i] = m - count[i] + (i == pre ? f1 : f0);
                if (count[i] < min1) {
                    min2 = min1;
                    min1 = count[i];
                    curMin = i;
                } else if (count[i] < min2) {
                    min2 = count[i];
                }
            }
            f0 = min1; f1 = min2; pre = curMin;
        }
        return f0;
    }
};