1457. Pseudo-Palindromic Paths in a Binary Tree

Posted on Edited on In

1457. Pseudo-Palindromic Paths in a Binary Tree

Description

Given a binary tree where node values are digits from 1 to 9. A path in the binary tree is said to be pseudo-palindromic if at least one permutation of the node values in the path is a palindrome.

Return the number of pseudo-palindromic paths going from the root node to leaf nodes.

Example 1:

1
2
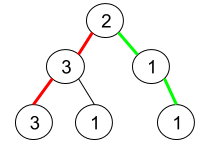
3
Input: root = [2,3,1,3,1,null,1]
Output: 2
Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the red path [2,3,3], the green path [2,1,1], and the path [2,3,1]. Among these paths only red path and green path are pseudo-palindromic paths since the red path [2,3,3] can be rearranged in [3,2,3] (palindrome) and the green path [2,1,1] can be rearranged in [1,2,1] (palindrome).

Example 2:

1
2
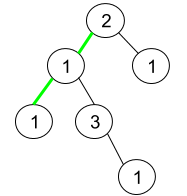
3
Input: root = [2,1,1,1,3,null,null,null,null,null,1]
Output: 1
Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the green path [2,1,1], the path [2,1,3,1], and the path [2,1]. Among these paths only the green path is pseudo-palindromic since [2,1,1] can be rearranged in [1,2,1] (palindrome).

Example 3:

1
2
Input: root = [9]
Output: 1

Constraints:

  • The number of nodes in the tree is in the range [1, 10^5].
  • 1 <= Node.val <= 9

Hints/Notes

  • traverse the tree

Solution

Language: C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int count[10] = {0};
    int res = 0;

    int pseudoPalindromicPaths (TreeNode* root) {
        if (!root) {
            return res;
        }
        count[root->val]++;
        if (!root->left && !root->right) {
            int odd_count = 0;
            for (int i = 0; i < 10; i++) {
                if (count[i] % 2 == 1) {
                    odd_count++;
                }
            }
            if (odd_count <= 1) {
                res++;
            }
        }
        if (root->left) pseudoPalindromicPaths(root->left);
        if (root->right) pseudoPalindromicPaths(root->right);
        count[root->val]--;
        return res;
    }
};