1514. Path with Maximum Probability

Posted on Edited on In

1514. Path with Maximum Probability

Description

Difficulty: Medium

Related Topics: Array, Graph, Heap (Priority Queue), Shortest Path

You are given an undirected weighted graph of n nodes (0-indexed), represented by an edge list where edges[i] = [a, b] is an undirected edge connecting the nodes a and b with a probability of success of traversing that edge succProb[i].

Given two nodes start and end, find the path with the maximum probability of success to go from start to end and return its success probability.

If there is no path from start to end, return 0. Your answer will be accepted if it differs from the correct answer by at most 1e-5.

Example 1:

1
2
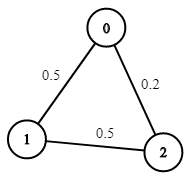
3
Input: n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2
Output: 0.25000
Explanation: There are two paths from start to end, one having a probability of success = 0.2 and the other has 0.5 * 0.5 = 0.25.

Example 2:

1
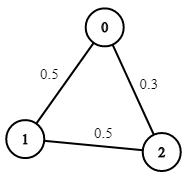
2
Input: n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], start = 0, end = 2
Output: 0.30000

Example 3:

1
2
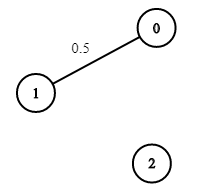
3
Input: n = 3, edges = [[0,1]], succProb = [0.5], start = 0, end = 2
Output: 0.00000
Explanation: There is no path between 0 and 2.

Constraints:

  • 2 <= n <= 10^4
  • 0 <= start, end < n
  • start != end
  • 0 <= a, b < n
  • a != b
  • 0 <= succProb.length == edges.length <= 2*10^4
  • 0 <= succProb[i] <= 1
  • There is at most one edge between every two nodes.

Hints/Notes

  • Dijkstra algorithm
  • Since the algorithm requires positive edge weights, when dijkstra algorithm reaches the
    destination, we can early return since the accumulation of edge labels along any path must
    have a monotonically non-decreasing partial order

Solution

Language: C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
class Solution {
public:
    vector<vector<pair<int, double>>> graph;
    vector<double> probs;

    double maxProbability(int n, vector<vector<int>>& edges, vector<double>& succProb, int start_node, int end_node) {
        graph = vector<vector<pair<int, double>>>(n, vector<pair<int, double>>());
        probs = vector<double>(n, 0);
        auto cmp = [](pair<double, int> lhs, pair<double, int> rhs) {
            return lhs.first < rhs.first;
        };
        priority_queue<pair<double, int>, vector<pair<double, int>>, decltype(cmp)> pq(cmp);
        buildGraph(edges, succProb);
        pq.push({1, start_node});
        while (!pq.empty()) {
            auto point = pq.top();
            pq.pop();
            double prob = point.first;
            int index = point.second;
            if (index == end_node) {
                return prob;
            }
            if (probs[index] > prob) {
                continue;
            }
            for (auto edge : graph[index]) {
                int nextPoint = edge.first;
                double nextProb = edge.second;
                nextProb = prob * nextProb;
                if (nextProb > probs[nextPoint]) {
                    probs[index] = prob;
                    pq.push({nextProb, nextPoint});
                }
            }
        }
        return probs[end_node];
    }

    void buildGraph(vector<vector<int>>& edges, vector<double>& succProb) {
        int size = edges.size();
        for (int i = 0; i < size; i++) {
            auto edge = edges[i];
            int p1 = edge[0];
            int p2 = edge[1];
            double prob = succProb[i];
            graph[p1].push_back({p2, prob});
            graph[p2].push_back({p1, prob});
        }
    }
};