261. Graph Valid Tree

Posted on Edited on In

261. Graph Valid Tree

Description

Difficulty: Medium

Related Topics: Depth-First Search, Breadth-First Search, Union Find, Graph

You have a graph of n nodes labeled from 0 to n - 1. You are given an integer n and a list of edges where edges[i] = [ai, bi] indicates that there is an undirected edge between nodes ai and bi in the graph.

Return true if the edges of the given graph make up a valid tree, and false otherwise.

Example 1:

1
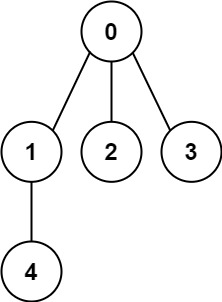
2
Input: n = 5, edges = [[0,1],[0,2],[0,3],[1,4]]
Output: true

Example 2:

1
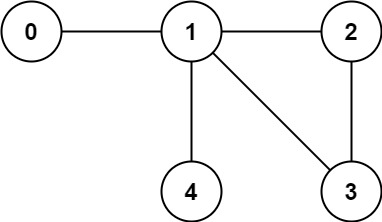
2
Input: n = 5, edges = [[0,1],[1,2],[2,3],[1,3],[1,4]]
Output: false

Constraints:

  • 1 <= n <= 2000
  • 0 <= edges.length <= 5000
  • edges[i].length == 2
  • 0 <= ai, bi < n
  • ai != bi
  • There are no self-loops or repeated edges.

Hints/Notes

  • 2023/09/03
  • Union find
  • A valid tree doesn’t have a cycle, and there’s only one component
  • premium

Solution

Language: C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public:
    vector<int> parent;
    int count;

    bool validTree(int n, vector<vector<int>>& edges) {
        for (int i = 0; i < n; i++) {
            parent.push_back(i);
        }
        count = n;
        for (auto edge : edges) {
            int p = edge[0];
            int q = edge[1];
            int rootP = find(p);
            int rootQ = find(q);
            if (rootP == rootQ) {
                return false;
            } else {
                parent[rootP] = rootQ;
                count--;
            }
        }

        return count == 1;
    }

    int find(int node) {
        if (parent[node] != node) {
            parent[node] = find(parent[node]);
        }
        return parent[node];
    }
};