323. Number of Connected Components in an Undirected Graph

Posted on Edited on In

323. Number of Connected Components in an Undirected Graph

Description

Difficulty: Medium

Related Topics: Depth-First Search, Breadth-First Search, Union Find, Graph

You have a graph of n nodes. You are given an integer n and an array edges where edges[i] = [ai, bi] indicates that there is an edge between ai and bi in the graph.

Return the number of connected components in the graph.

Example 1:

1
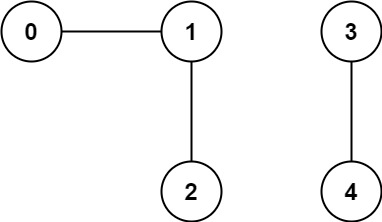
2
Input: n = 5, edges = [[0,1],[1,2],[3,4]]
Output: 2

Example 2:

1
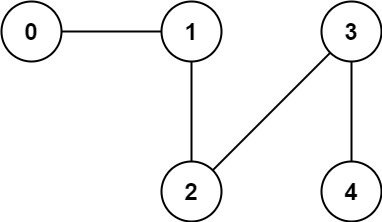
2
Input: n = 5, edges = [[0,1],[1,2],[2,3],[3,4]]
Output: 1

Constraints:

  • 1 <= n <= 2000
  • 1 <= edges.length <= 5000
  • edges[i].length == 2
  • 0 <= ai <= bi < n
  • ai != bi
  • There are no repeated edges.

Hints/Notes

  • 2023/09/02
  • union find
  • if the edge’s two nodes are not connected previously, then minus the number of component since they are connected now
  • premium

Solution

Language: C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    vector<int> roots;

    int countComponents(int n, vector<vector<int>>& edges) {
        roots = vector<int>(n, 0);

        iota(roots.begin(), roots.end(), 0);

        int num = n;
        for (auto pair : edges) {
            int p = pair[0];
            int q = pair[1];
            int rootP = find(p);
            int rootQ = find(q);
            if (rootP != rootQ) {
                roots[rootP] = rootQ;
                num--;
            }
        }

        return num;
    }

    int find(int node) {
        if (roots[node] != node) {
            roots[node] = find(roots[node]);
        }
        return roots[node];
    }
};